Новая итерационная схема позволяет эффективно решать сложную модель Хаббарда, открывая перспективы для моделирования материалов на квантовых компьютерах.
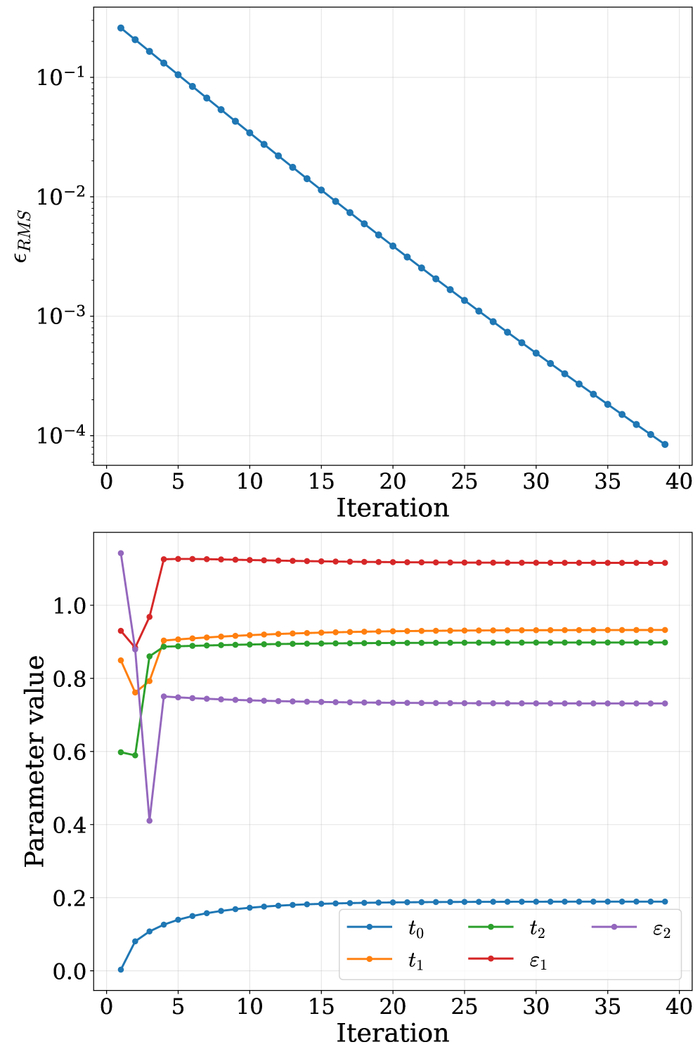
Итеративный процесс подгонки демонстрирует сходимость даже в окрестности металл-диэлектрического перехода, при различных значениях энергии взаимодействия U=2, 4, 6, 8, что подтверждается быстрой стабилизацией пяти независимых параметров ванны {t₀, t₁, t₂, ε₁, ε₂} - менее чем за 20-30 итераций - и измеряется как среднеквадратичная ошибка εRMS между последовательными гибридизационными функциями.
Предложена схема итерационного решения модели Хаббарда в рамках динамической теории поля, демонстрирующая возможность получения достаточно точных результатов при небольшом числе вспомогательных сайтов.
Традиционные подходы к решению задачи многих тел в сильных корреляциях, такие как теория динамического среднего поля (DMFT), часто требуют значительных вычислительных ресурсов. В работе, озаглавленной 'Real-Time Iteration Scheme for Dynamical Mean-Field Theory: A Framework for Near-Term Quantum Simulation', предложен новый итерационный метод, работающий непосредственно в реальном времени, что позволяет снизить вычислительную сложность. Показано, что предложенная схема позволяет достичь удовлетворительной точности при решении модели Хаббарда, используя ограниченное число сайтов для дискретизации функции гибридизации. Открывает ли это путь к реализации алгоритмов DMFT на перспективных квантовых вычислительных платформах и позволит ли исследовать фазовые переходы, такие как переход металл-диэлектрик, с беспрецедентной точностью?
Трудности изучения сильно коррелированных материалов
Исследование материалов, в которых электроны сильно взаимодействуют друг с другом, представляет собой серьезную задачу для современных методов электронной структуры. Это взаимодействие, известное как сильная корреляция, создает так называемую «многочастичную проблему», делая точные расчеты чрезвычайно сложными. Хотя упрощенная модель Хаббарда позволяет уловить суть этих взаимодействий, ее применение в многомерных системах часто оказывается вычислительно невозможным. Преодоление этих ограничений необходимо для понимания возникновения коллективных явлений, таких как переход металл-диэлектрик, когда материал меняет свои электрические свойства, и для разработки новых материалов с заданными характеристиками. Изучение этих взаимодействий требует новых подходов и вычислительных методов, способных справиться со сложностью многочастичных систем.
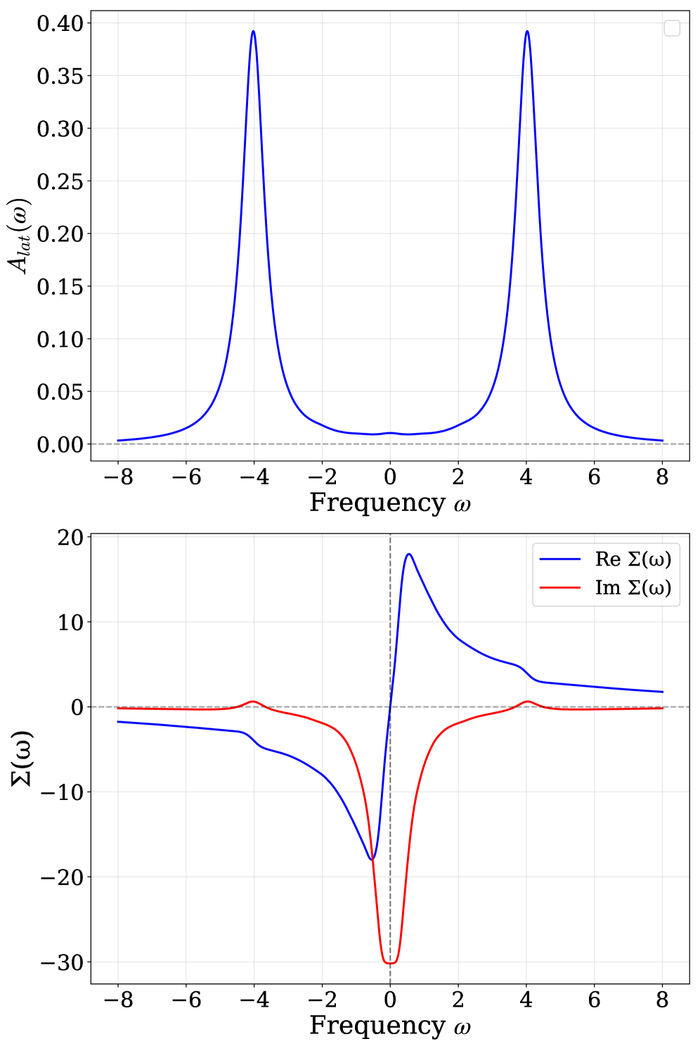
Изменение спектральных свойств отдельной частицы при переходе металл-изолятор при различных значениях взаимодействия U демонстрирует эволюцию от коррелированного металла с выраженным пиком квазичастиц, через режим сосуществования с трехпиковой структурой, к полностью зазоренному моттовскому изолятору с переносом спектрального веса в высокоэнергетические хаббардовские полосы, что подтверждается поведением локальной самоэнергии Σ(ω), характеризующейся минимумом модуля в ω=0 в металлических фазах и расходимостью реальной и мнимой частей при ω=0 в моттовском изоляторе.
От сложности к единичной проблеме: как работает DMFT
Динамическая теория среднего поля (DMFT) позволяет упростить изучение сложных систем, состоящих из множества взаимодействующих частиц. Вместо того чтобы пытаться решить задачу для всех частиц одновременно, DMFT сосредотачивается на электронной среде вокруг каждой отдельной частицы, рассматривая её как своего рода «загрязнение» в материале. Это «загрязнение» помещается в окружение, которое имитирует остальную часть системы, обычно представляемое в виде сложной решетки, называемой решеткой Бете. Решение этой упрощенной задачи для «загрязнения» дает информацию о том, как электроны ведут себя локально. Эти данные затем используются для уточнения модели окружающего материала, создавая цикл самосогласования. Благодаря этому подходу, DMFT позволяет понять сложные электронные свойства материалов, фокусируясь на локальном поведении частиц и их взаимодействии с окружением.
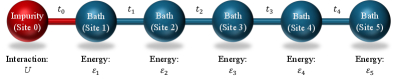
Эффективная модель Андерсона примеси представлена в виде линейной цепи, состоящей из взаимодействующей примеси (сайт 0) с кулоновским отталкиванием U и некоторой не взаимодействующей ванны из Nbₐₜₕ = 5 сайтов, параметризованных амплитудой перескока tᵢ и на-сайтовой энергией varepsilonᵢ.
Динамическая теория среднего поля: современный подход
Новая методика решения уравнений теории среднего поля (DMFT) использует прямой подход, работающий непосредственно во временной области, избегая сложных преобразований, необходимых при работе в частотной области. Ключевым элементом является представление задачи примеси в виде одномерной цепочки, что позволяет эффективно её моделировать на компьютере. Для точного решения этой упрощенной задачи примеси используется метод точной диагонализации, который служит эталоном для будущих квантовых вычислений. Важную роль играет параметр затухания, подавляющий нежелательные колебания во временных расчетах и обеспечивающий стабильность процесса. Данный метод демонстрирует устойчивую сходимость всего за 20-30 итераций, используя минимальный размер вспомогательной системы в 5 элементов, что открывает перспективы для реализации на квантовом оборудовании.
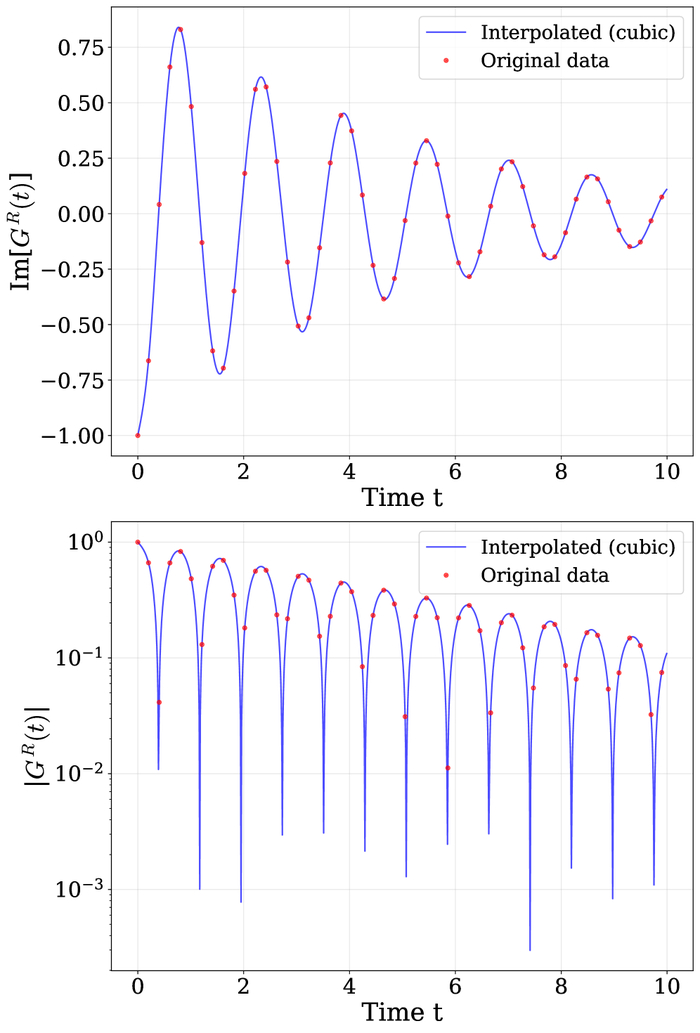
Кубическая интерполяция функции Грина примеси Gᴿᵢₘₚ(t) для различных значений взаимодействия U (2, 4, 6, 8) демонстрирует изменение характера затухания от медленного при U=2 до быстрых, устойчивых осцилляций при U=8, что отражает формирование высокоэнергетических хаббардовских полос.
От локального к глобальному: Расширяя возможности DMFT
Современные исследования выходят за рамки стандартной теории динамических средних полей (DMFT), стремясь описать системы, где взаимодействие между электронами не ограничивается ближайшими соседями. Развитие метода, известное как DMFT в реальном пространстве, позволяет изучать неоднородность материалов и ее влияние на электронные свойства, рассматривая изменения характеристик в разных точках образца. Комбинирование этого подхода с приближением когерентного потенциала (CPA) открывает возможность исследовать влияние беспорядка на электронные корреляции, что особенно важно для понимания поведения материалов с дефектами или примесями. Эти усовершенствованные методы DMFT значительно облегчают анализ формирования хаббардовских зон - характерных энергетических полос, определяющих свойства сильно коррелированных материалов, и позволяют глубже понять физические процессы, происходящие в таких сложных системах.
Представленная работа демонстрирует стремление к упрощению сложных вычислений в рамках теории динамического среднего поля. Авторы предлагают итерационную схему во временной области, позволяющую достичь приемлемой точности решения модели Хаббарда с использованием ограниченного числа вспомогательных сайтов. Этот подход, ориентированный на практическую реализацию на квантовых компьютерах ближайшего поколения, находит отклик в словах Рене Декарта: «Я думаю, следовательно, существую». Подобно тому, как философ стремился к ясным и недвусмысленным принципам, так и данное исследование направлено на создание эффективного и прозрачного метода решения сложной физической задачи, избегая излишней сложности и сосредотачиваясь на сути явления - фазовом переходе Мотта.
Что дальше?
Представленная схема итераций во временной области, несомненно, представляет собой шаг к сокращению вычислительной сложности, неизбежно сопутствующей методу Динамической Теории Среднего Поля. Однако, эйфория от уменьшения необходимого числа ванновых сайтов должна быть умеренной. Сам факт необходимости итераций, даже ускоренных, указывает на фундаментальную проблему: поиск истинного решения, а не его приближения, остается нерешенным. Упрощение модели, как и любое упрощение, неизбежно вносит погрешности, а вопрос о допустимом уровне этих погрешностей для различных физических явлений требует тщательного анализа.
Попытки непосредственной реализации на квантовых компьютерах ближайшего будущего, хотя и заманчивы, столкнутся с неизбежными ограничениями, связанными с когерентностью кубитов и точностью операций. Поэтому, вероятно, более продуктивным направлением станет разработка гибридных алгоритмов, сочетающих классические и квантовые вычисления. В таком подходе квантовый компьютер может выполнять наиболее трудоемкие части вычислений, в то время как классические алгоритмы обеспечивают контроль и коррекцию ошибок.
В конечном счете, истинная ценность данной работы заключается не в достижении абсолютной точности, а в стимулировании дальнейшего поиска более элегантных и эффективных методов решения сложных задач многочастичной физики. Потому что, в конце концов, простота - не ограничение, а признак глубокого понимания.