Новый подход к коррекции ошибок в квантовых вычислениях
Автор: Денис Аветисян
Исследователи разработали систему автоматической оптимизации последовательности измерений синдромов, позволяющую значительно снизить вероятность логических ошибок в квантовых вычислениях.
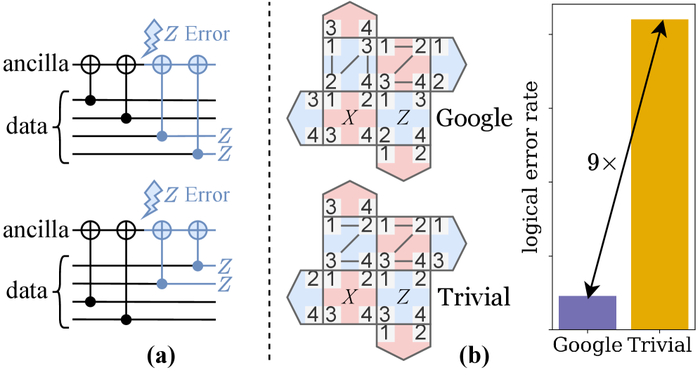
Исследование демонстрирует, что различные схемы выполнения измерения синдрома ZZZZZ в поверхностном коде квантовой коррекции ошибок приводят к разным показателям логических ошибок, при этом временные шаги выполнения проверок Паули между кубитами данных и вспомогательными кубитами определяют эффективность каждой схемы.
В статье представлен фреймворк AlphaSyndrome, использующий метод Монте-Карло поиска по дереву (MCTS) для эффективного планирования измерений синдромов в кодах квантовой коррекции ошибок.
Несмотря на критическую важность квантовой коррекции ошибок (QEC) для масштабируемых квантовых вычислений, оптимизация последовательности измерений синдромов остается сложной задачей, определяющей эффективность и стоимость реализации. В статье 'AlphaSyndrome: Tackling the Syndrome Measurement Circuit Scheduling Problem for QEC Codes' представлена автоматизированная платформа AlphaSyndrome, использующая метод Монте-Карло поиска по дереву (MCTS) для оптимизации планирования измерений синдромов в кодах со взаимно коммутирующими стабилизаторами. Разработанный подход позволяет снизить логическую частоту ошибок на 80.6% в среднем, превосходя существующие методы и демонстрируя конкурентоспособность с ручными решениями для поверхностных кодов. Какие перспективы открывает автоматическая оптимизация схем измерений синдромов для реализации надежных и масштабируемых квантовых вычислений на различных архитектурах?
Хрупкость Квантовой Информации
Квантовые вычисления обещают революционные возможности, однако их фундаментальная природа делает их крайне уязвимыми к ошибкам, возникающим из-за явления декогеренции - потери квантовых свойств из-за взаимодействия с окружающей средой. Для защиты этих хрупких квантовых состояний необходима квантовая коррекция ошибок (ККО). Традиционные методы коррекции ошибок полагаются на измерение синдрома - процесса, позволяющего выявить и исправить ошибки, но сам этот процесс может быть осложнен распространением ошибок, когда попытка исправления одной ошибки приводит к появлению новых. Разработка эффективных и надежных методов ККО является ключевой задачей для реализации практических квантовых вычислений, способных решать задачи, непосильные для классических компьютеров.
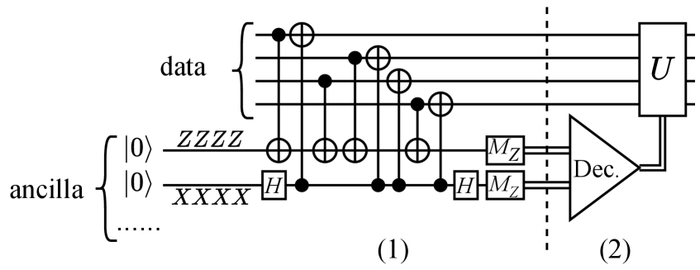
Процесс коррекции ошибок в коде КЭКК включает измерение синдрома и последующую декодирование с коррекцией.
Коды Стабилизаторов: Основа Квантовой Коррекции Ошибок
Коды стабилизаторов представляют собой значимый класс кодов квантовой коррекции ошибок (ККО), определяющих процесс исправления ошибок посредством набора стабилизирующих операторов. В рамках этого семейства особое внимание уделяется кодам поверхностного типа и цветовым кодам, которые активно исследуются благодаря своим свойствам устойчивости к ошибкам. Эффективность этих кодов напрямую зависит от точного и быстрого выполнения измерений синдрома - процедуры, позволяющей выявить и локализовать ошибки в квантовой информации, не нарушая её состояние. По сути, измерение синдрома позволяет понять, где произошла ошибка, не "подглядывая" за самой квантовой информацией, что принципиально важно для сохранения её целостности.
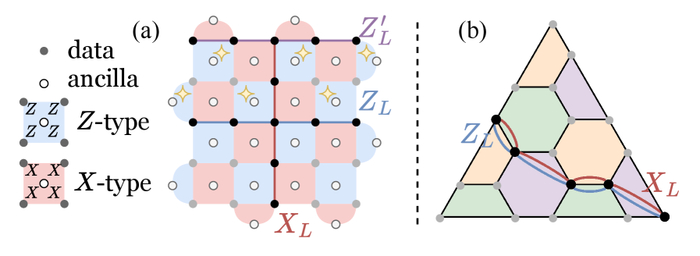
На представленных кодах поверхности XX и гексагональных кодах цвета, каждый многоугольник представляет собой XX и ZZ стабилизатор, при этом два ZLZL на коде поверхности эквивалентны при умножении на помеченные стабилизаторы.
АльфаСиндром: Интеллектуальное Планирование для Улучшенной Коррекции Квантовых Ошибок
Разработанный подход АльфаСиндром представляет собой новую систему, использующую метод Монте-Карло с деревом поиска (MCTS) для оптимизации порядка измерений синдромов - ключевого этапа в процессе квантовой коррекции ошибок. В отличие от традиционных методов, основанных на поиске кратчайшего пути, АльфаСиндром учитывает специфические характеристики ошибок, динамически адаптируя последовательность измерений. Такой подход, основанный на анализе данных, позволяет добиться впечатляющего снижения вероятности логических ошибок - в среднем на 80.6% - при использовании различных квантовых кодов и декодеров. Более того, АльфаСиндром позволяет значительно сократить требуемый объем вычислительных ресурсов - на 20-90% - за счет уменьшения необходимой "расстояния кода", что делает процесс обнаружения и исправления ошибок значительно эффективнее и практичнее.
Расшифровка и Производительность в Реальных Условиях
Исследование демонстрирует, что методика AlphaSyndrome, используемая совместно с классическим декодером, существенно снижает частоту логических ошибок. Особенно заметен эффект в ситуациях, имитирующих несовершенство реального квантового оборудования, где вероятность ошибок неоднородна. Результаты показывают, что AlphaSyndrome достигает производительности, сопоставимой с эталонными показателями Google для ротированных поверхностных кодов. Применительно к коду Bivariate Bicycle, AlphaSyndrome обеспечивает снижение частоты логических ошибок на 44% при использовании декодирования BP-OSD и на 10% при использовании Unionfind декодирования. Максимальное снижение частоты логических ошибок, зафиксированное во всех протестированных конфигурациях, составило впечатляющие 96.2%, что свидетельствует о значительном прогрессе в области коррекции квантовых ошибок.
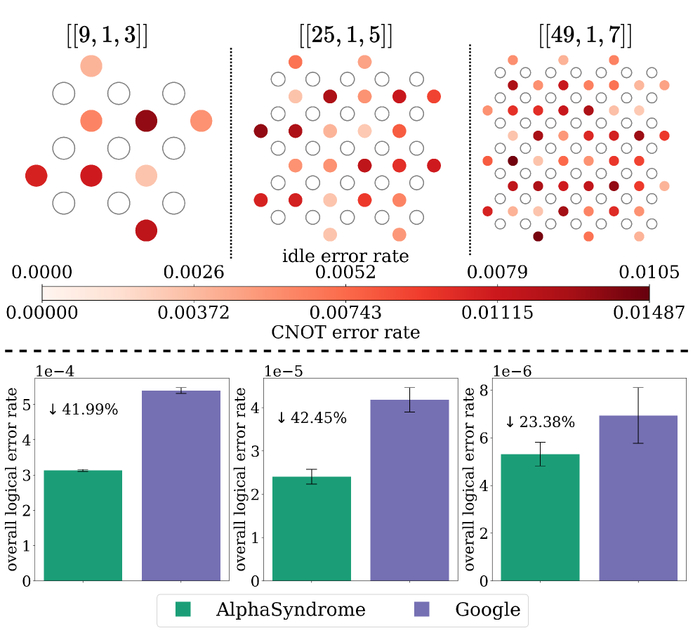
Сравнение AlphaSyndrome и Google показало, что при использовании неравномерной модели ошибок, AlphaSyndrome демонстрирует более низкие общие логические ошибки, особенно при повышенных ошибках на вспомогательных кубитах.
Исследование, представленное в данной работе, демонстрирует стремление к построению устойчивых алгоритмов для квантовой коррекции ошибок. Подход, основанный на Monte Carlo Tree Search (MCTS) для оптимизации планирования схем измерения синдрома, акцентирует внимание на минимизации скорости логических ошибок - ключевом показателе эффективности квантовых вычислений. Как однажды заметил Джон фон Нейманн: «В науке не существует абсолютной истины, только лучшие приближения.» Эта фраза перекликается с сутью представленного исследования, ведь даже самые передовые алгоритмы квантовой коррекции ошибок представляют собой не идеальное решение, а лишь наилучшее на текущий момент приближение к стабильности и надежности квантовых вычислений. Пусть N стремится к бесконечности - что останется устойчивым? В данном случае, это стремление к минимизации ошибок и повышению точности квантовых операций.
Куда же дальше?
Представленная работа, безусловно, демонстрирует эффективность подхода, основанного на Monte Carlo Tree Search, для оптимизации расписания измерений синдромов в квантовой коррекции ошибок. Однако, триумф алгоритма над существующими методами не должен затуманивать фундаментальные вопросы. Детерминированность результата, воспроизводимость - вот краеугольные камни любой научной работы. Успехи, достигнутые в симуляциях, должны быть подтверждены на реальном квантовом оборудовании, где шум и несовершенство аппаратуры вносят свои коррективы в математическую чистоту расчетов.
Особое внимание следует уделить масштабируемости предложенного подхода. С увеличением числа кубитов и сложности кода коррекции ошибок, вычислительная сложность MCTS возрастает экспоненциально. Необходимо исследовать возможности применения гибридных алгоритмов, сочетающих MCTS с другими методами оптимизации, или разработать новые эвристики, позволяющие эффективно сократить пространство поиска. В противном случае, элегантность решения окажется недостижимой в практических реализациях.
И, наконец, не стоит забывать о более глубоких вопросах. Оптимизация расписания измерений - лишь один из аспектов квантовой коррекции ошибок. Необходимо разрабатывать новые коды, устойчивые к различным типам шума, и исследовать возможности динамической адаптации стратегии коррекции ошибок в зависимости от характеристик аппаратуры. Истинная элегантность заключается не в оптимизации существующего, а в создании принципиально нового.
Полный обзор с формулами: lospopadosos.com/optimizacziya-kvantovoj-korrekczii-oshibok-alphasyndrome-i-poisk-idealnogo-raspisaniya
Оригинал статьи: https://arxiv.org/pdf/2601.12509.pdf
Связаться с автором: linkedin.com/in/avetisyan