В пивной лавке г. Слоуты Глуховского уезда сидела группа местных селян. К ним присел лесной объездчик соседней экономии землевладельца фон-дер-Бриггене ингуш Хочас Ахриев. Ахриев стал хвастаться: «Вот хотите, держу пару на бутылку пива, что убью крестьянина, и ничего мне за него не будет… Хотите, так вот здесь же в пивной убью того дядьку».В углу пивной угрюмо сидел и пил пиво местный крестьянин Лисица. Собеседники согласились на это пари… Ахриев подошел к Лисице, и не говоря ни слова, выхватил кинжал и набросился на мужика… Несколько мгновений длилась упорная, жестокая борьба между Ахриевым и Лисицей. Скоро кинжал ингуша очутился в руках Лисицы. Еще одно мгновение, и Ахриев лежал уже на полу с распоротым животом…По дороге в больницу ингуш скончался. «Орловская жизнь». 1913. № 65

Наряду с военной службой Александр Бригген сотрудничал в «Военном журнале», издававшемся в 1816—1819 годах органе «Общества военных людей», организованном при штабе гвардейского корпуса. Задачами общества были обобщения и популяризация опыта Отечественной войны и заграничных походов; его редактором был Фёдор Николаевич Глинка. Бригген составил исторические заметки «Анекдот», «Записки Кайя Юлия Кесаря», «Происхождение Павла I».

Это классическая задача теории вероятностей, известная как "Парадокс дней рождения".

Ответ зависит от размера компании. Парадокс заключается в том, что вероятность совпадения дней рождения растет гораздо быстрее, чем нам кажется интуитивно.

Давайте рассчитаем вероятность для разного количества человек.

Краткий ответ (для компании из 23 человек)

Вероятность того, что хотя бы у двух людей из 23 день рождения совпадет, составляет примерно 50.7%.

Это уже больше половины! Именно поэтому это называют парадоксом — наша интуиция часто сильно занижает эту вероятность.

Как рассчитывается вероятность?

Проще всего рассчитать вероятность противоположного события — что все дни рождения разные, а затем вычесть эту вероятность из 1.

Формула выглядит так:

P(совпадение) = 1 - P(все дни рождения разные)

Вероятность того, что все дни рождения в группе из n человек различны, рассчитывается по формуле:

P(все разные) = (365/365) * (364/365) * (363/365) * ... * ((365 - n + 1)/365)

Таблица вероятностей для разного размера компании

Вот как вероятность меняется в зависимости от количества человек (n):

Количество человек (n) Вероятность совпадения
5 ~2.7%
10 ~11.7%
23 ~50.7%
30 ~70.6%
40 ~89.1%
50 ~97.0%
60 ~99.4%

Пример расчета для компании из 10 человек

1. Первый человек может родиться в любой день года: 365/365 = 1.
2. Второй человек должен родиться в другой день: 364/365.
3. Третий человек должен родиться не в те же дни, что и первые два: 363/365.
4. ... и так далее до десятого человека: 356/365.

Перемножаем эти вероятности, чтобы найти вероятность того, что все дни рождения разные:
P(все разные) = (365/365) * (364/365) * ... * (356/365) ≈ 0.883

Вероятность хотя бы одного совпадения:
P(совпадение) = 1 - 0.883 = 0.117или 11.7%.

Важные уточнения

1. "Хотя бы у двух": Мы считаем вероятность хотя бы одного совпадения. Это включает в себя и вариант, когда совпадают дни рождения у ровно одной пары, и когда совпадают у трех человек и т.д.
2. Упрощения модели: В расчете мы не учитываем високосные годы (29 февраля), предполагаем, что все дни рождения равновероятны, и не учитываем близнецов.
3. Для вашего вопроса: Если вы имели в виду конкретно, что в компании есть ровно два человека с совпадающим днем рождения, а у всех остальных дни рождения уникальны, то вероятность будет немного ниже, чем приведенные выше цифры. Однако на практике почти всегда интересует вероятность "хотя бы одного совпадения".

В дружеской компании, скажем, из 10 человек, вероятность совпадения дней рождения уже заметна (~12%), а в компании из 23 человек шансы "за или против" практически равны (около 50/50).

Экономист Пол Самуэльсон однажды прочитал где-то, что трус - это тот, кто не ставит при коэффициенте 2 к 1. Однажды он поделился этим соображением с коллегами за обедом.

«Совсем как ты, Кери» - обратился Пол к экономическому историку по имени Э. Кери Браун и предложил пари. “Давай подбросим монету, если выпадет решка, то твой выигрыш составит 200$, если орел, то проигрыш будет равняться 100$”.

Это выгодный спор с математической точки зрения. Ожидаемый выигрыш составляет 50 долларов.  Добавим немного контекста. Самуэльсон предложил пари в 1963 году. Это как спорить на 1000 долларов в 2025 году, если учитывать инфляцию и покупательную способность..

Представьте, Вам предлагают подбросить монетку. Решка, и Вы в плюсе на 200 тысяч рублей, Орел - Вы должны 100 тысяч. Согласились бы? А если честно?

Вот и Керри Браун не согласился.

«Я не буду спорить, потому что буду сокрушаться по поводу потерянных 100$ больше, чем радоваться выигрышу в 200$».

Этот феномен называется "неприятие потерь" (loss aversion).

В экономике существует модель рационального агента — человека, который всегда принимает решения, максимизируя свою ожидаемую полезность. Такой “человек-калькулятор” оценивает все возможные исходы и их вероятности, а затем принимает решение, если математическое ожидание сделки положительно.

Браун продемонстрировал, что страх потери иногда оказывается сильнее рационального выбора. И котики не могут его за это осуждать.

Керри Браун отказался спорить, потому что потеря $100 для него психологически тяжелее, чем радость выигрыша $200. Хотя, заметил Кери “я бы согласился сыграть в такую игру, если она будет продолжаться 100 раундов”.

100 раундов лучше, чем 1?

Браун рассуждал следующим образом: если сыграть много раз, то средний результат будет близок к математическому ожиданию (+$50 за каждый раунд), а значит, вероятность убытков почти отсутствует.

Самуэльсон крепко задумался и как настоящий экономист, скоро написал научную статью. В своей работе профессор обосновал, почему Керри Браун поступает нерационально, отказываясь от одной игры и соглашаясь на 100.

Вот как рассуждал Самуэльсон. Допустим, Браун соглашается сыграть 100 раундов. Однако после того, как сыграны 99 раундов, Самуэльсон предлагает ему остановиться, т. е. оставляет последний раунд на выбор Брауна. Как поступит Браун? Что ж, нам известно, что он не любит спорить, а речь идет именно о таком случае, поэтому он выбирает прекратить игру. Теперь представим, что то же самое произошло после 98 сыгранных раундов. Мы говорим Брауну, что от каждого из оставшихся двух раундов можно отказаться. Как он поступит? Как профессиональный экономист, он начнет думать ретроспективно, т. е. анализировать ситуацию начиная с  конца и продвигаясь к началу.

В ходе своих рассуждений он поймет, что когда речь пойдет о 100-м раунде, то это будет игра ва-банк, и он от нее откажется. А это будет означать, что 99-й раунд тоже является игрой ва-банк, которая ему не по душе, поэтому он откажется играть и 99-й раунд. Но, если следовать этой логике в отношении каждого раунда, то в результате получится, что Браун не станет играть ни одного раунда, даже самого первого. Отсюда вывод Самуэльсона: если вы не хотите играть ва-банк за один раунд, то не станете играть и много раундов.

Ричард Талер. Новая поведенческая экономика

Если один раз не приносит пользы, то почему она появится после сотого повторения?

Самуэльсон считал, что Керри Браун неправильно понимает закон больших чисел. Когда Браун предложил 100 подбрасываний монетки, то проигнорировал возможность потерять огромную сумму денег.

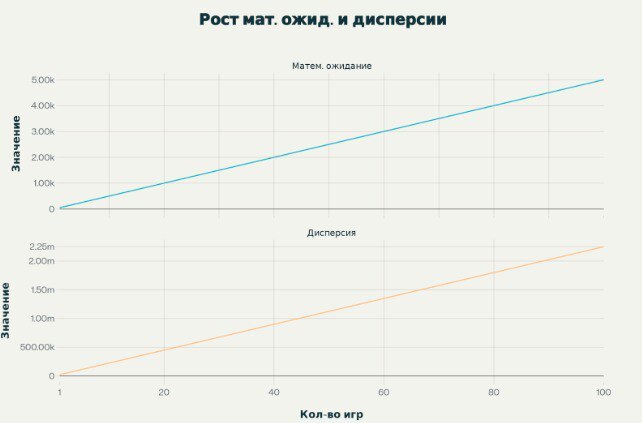
При одной игре вероятность проиграть $100 равна 50%. С увеличением количества игр шансы потерять деньги уменьшаются, а возможные суммы выигрыша растут. В среднем за 100 игр игрок получит $5000 прибыли.

Но, если Вы проиграете 100 игр подряд, то придется отдать $10000 (а это миллион долларов в 2025 году). Вероятность этого события составляет 0,00000000000000000000000000000079%.

Повторяя случайную игру много раз, средний выигрыш или проигрыш за игру становится ближе к матожиданию, однако сам разброс возможных итогов (то есть дисперсия суммы всех результатов) увеличивается с каждой игрой.

И если Керри Браун будет испытывать “чувство потери” от проигрыша 100 долларов, то крайне малая вероятность катастрофических потерь тоже должна учитываться .

Новый взгляд на пари и узкий фрейминг

История с пари на этом не закончилась. В 1993 году, анализируя сценарий игры Самуэльсона, экономисты Шломо Бенарци и Ричард Талер пришли к выводу, что Самуэльсон прав только наполовину.

И Кэри Браун, и Самуэльсон стали жертвами узкого фрейминга.

Браун рассматривал единичную ставку как отдельное решение, не учитывая ее в контексте общего благосостояния.

Самуэльсон строил свои доказательства, исходя из предположения, что каждый раунд игры - это отдельная ставка.Однако, экономист не учел, что если игра состоит из множества подбрасываний монеты, то нет никакого смысла рассматривать их изолированно друг от друга. 

«Агрегированная игра из 100 ставок 50-50 проиграть $100/выиграть $200 имеет ожидаемый доход $5,000, с лишь 1/2,300 шансом потерять любые деньги и всего лишь 1/62,000 шансом потерять более $1,000. Хороший юрист мог бы объявить вас юридически невменяемым за отказ от этой игры»

Ричард Талер. Новая поведенческая экономика

Экономисты Шломо Бенарци и Ричард Талер повторили пари Самуэльсона. Они предлагали участникам эксперимента подбросить монетку и выиграть 200$, если выпадет орел, или проиграть 100$, если выпадет решка. Как и Керри Браун больше половины участников отказались играть ссылаясь на “неприятие потерь”.

Бенарци и Талер проводили этот эксперимент в 1990-х годах и сумма спора была достаточно внушительной. $100 в 1990 году - это $246 в 2025 году по паритету покупательной способности.

Затем экономисты предложили подбросить монетку два раза. На это согласилось еще меньше добровольцев. Многие руководствовались логикой Пола Самуэльсона - “если мне не нужна одна ставка, игра, то зачем принимать вторую”?

Тогда Бенарци и Талер предложили следующую игру:

У вас есть 25% на выигрыш 400$, 50% на выигрыш 100$ и 25% на потерю 200$. Будете играть? Ответ под спойлером.

Хитрость в том, что экономисты объединили два броска монетки в одну ставку с тремя исходами.

В игре с двумя бросками у нас есть 4 равновероятных исхода.

• Орел + Орел (выиграли $200 + $200 = $400)

• Орел + Решка (выиграли $200, проиграли $100 = $100)

• Решка + Орел (проиграли $100, выиграли $200 = $100)

• Решка + Решка (проиграли $100 и еще $100 = –$200)

Каждый исход имеет одинаковую вероятность — 1 из 4, или 25%. Орел + Решка и Решка + Орел приводят к одной и той же сумме (+$100), поэтому их вероятности складываются.

То есть, участникам также предлагалось 2 раза подбросить монетку, но количество желающих рискнуть сразу увеличилось в два раза. Шансы выиграть или проиграть деньги остались теми же. Теперь участники воспринимали эти два броска как одну игру с положительным ожидаемым выигрышем — именно так, как надо было изначально.

Узкий фрейминг заставляет оценивать риски и выгоды в отрыве от общей картины. Расширение фрейма позволяет принимать более качественные экономические решения.

Подписывайтесь, чтобы не пропускать новые публикации.

Еще больше экономики и котиков в Телеграмме

#comment_365736931

@dzianiska тут опять интересное пари намечается. )