Введение

В индийской культурной традиции число 108 занимает положение почти «универсального маркера полноты». Оно регулярно встречается в самых разных контекстах: в ритуальной арифметике, в поздних каталогах священных текстов, в практике джапы (многократного повторения мантр), в тантрических и йогических схемах, а также в астрологических разложениях.

Однако сама по себе повторяемость этого числа в традиции ещё не даёт чёткого ответа на два ключевых вопроса. Во‑первых, почему именно 108 стало устойчивым «конечным» значением? Во‑вторых, какой конкретный смысл оно должно нести в рамках вычислимой модели различения?

В моем проекте этот вопрос переводится из плоскости интерпретаций и символических толкований в плоскость строгого формализма. Я ищу механизм, который порождает число 108 не на основе смысловых или культурных ассоциаций, а исключительно по структурным основаниям. При этом вывод числа должен быть строго обусловлен структурой универсальной янтры — полной таблицы бинарной операции PLUS, заданной на конечном множестве полярностей с фиксированной нейтралью.

В этом подходе число 108 должно появляться как неизбежный продукт комбинации четырёх элементов:

1. Строгих симметрий закона — автоморфизмов таблицы.

2. Орбитальной структуры действия этих симметрий на ненулевых полярностях.

3. Ориентации шага — различения элементов u и u^(-1).

4. Фазового замыкания как системы независимых координат по триадным орбитам.

Такой подход позволяет заранее исключить методологическую ошибку, которая возникает при недостаточном анализе многополярных таблиц конечной магмы.

Например, в шестиполярности L6 и семиполярности L7 можно обнаружить конфигурации, внешне схожие с «двумя тройками». Однако их происхождение принципиально различается: они формируются в разных слоях симметрий и на разных доменах.

Следовательно, если в обоих случаях получается число 108, это не указывает на структурную необходимость. Это скорее следствие смешения категорий — ошибочного отождествления структур, имеющих разную природу.

Мой метод предотвращает такую путаницу, выстраивая вывод числа 108 на чёткой структурной основе.

1. История числа 108

В ранней ведической традиции число 10 800 выступает как структурная величина (108×100), символизирующая полноту корпуса текстов и космоса. Важно: это не прямое указание в гимнах самхит, а традиционная рационализация, зафиксированная позднее — в брахманах (ритуальной прозе).

В постведический период стабилизируются два ключевых разложения числа 108:

• 54×2=108 — отражает принцип двойственности (мужское / женское, Шива / Шакти и т. п.): 54 как «половина полноты», умноженная на 2 для достижения завершённости;

• 12×9=108 — имеет астролого‑календарный смысл: 12 как цикл разметки (знаки зодиака, месяцы), 9 как внутренняя градация (планеты‑грахи, фазы).

Таким образом, 108 оформляется как стратифицированный канон — устойчивая схема, воспроизводимая в разных контекстах традиции.

Для моей инженерной задачи эта стратификация существенна по двум причинам:

1. Она демонстрирует, что число 108 практически всегда возникает как результат факторизации — то есть как произведение двух относительно простых механизмов, а не как первичное «сакральное» число, лишённое внутренней структуры. Это принципиально: перед нами не мистический символ, а вычислимая композиция.

2. Два ключевых разложения — 54 × 2 и 12 × 9 — органично вписываются в язык моего формализма:

• 2 соответствует ориентации шага (u против u^-1) — базовому различию направлений;

• 12 отражает число ориентированных базовых шагов на двух триадах (по 3 элемента в каждой): это комбинаторная размерность упорядоченных переходов;

• 9 задаёт фазовое замыкание на паре триад (Z3 × Z3) — структуру независимых фаз в произведении циклических групп;

• 54 выступает как фактор по ориентации — число видов без учёта направления (то есть «неориентированных» конфигураций).

Иными словами, традиционные «нумерологические каноны» оказываются слабыми культурными проекциями тех структурных объектов, которые в вычислимой модели выражаются строго: через орбиты действий симметрий и подгруппы соответствующей алгебраической системы.

Это позволяет перейти от символической интерпретации числа 108 к его конструктивному воспроизведению в рамках формальной схемы — исходя из симметрий, орбит и фазовых замыканий на конечном множестве полярностей.

2. Что такое янтра L7 в строго вычислимом смысле

Под семиполярностью L7 (в принятом каноне: SEMIPOLAR) понимается универсальная янтра следующего вида. Множество полярностей: P = {P0, P1, P2, P3, P4, P5, P6}, |P| = 7. Бинарная операция PLUS: P × P -> P задана полностью в виде таблицы (таблицы Кэли).

Нейтральный элемент e фиксируется кадром ZERO_Pk и проверяется по таблице: для всех a in P: e PLUS a = a и a PLUS e = a.

Ненулевой домен задаётся как X = P \ {e}, |X| = 6.

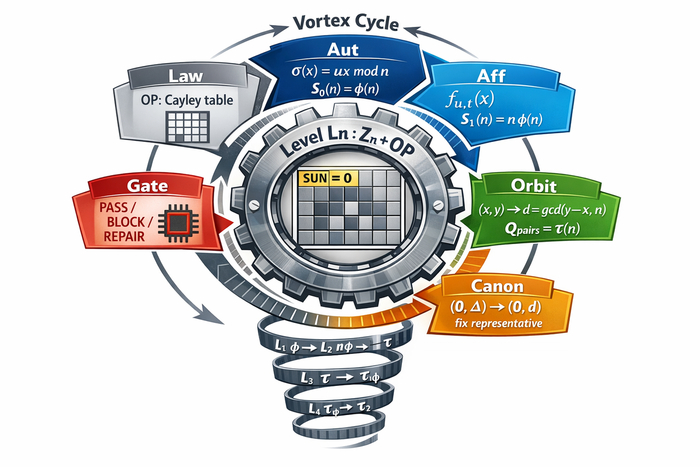
3. Симметрии L7

Ниже приведена «точка фиксации», которую полезно держать в поле зрения перед обсуждением чисел 12/54/108. Речь идёт не о метафоре, а о конкретном вычислимом объекте: универсальной янтре семиполярности, полностью задаваемой таблицей бинарной операции PLUS на конечном множестве состояний.

1) Где лежит янтра L7 в архиве и что означает кадр

В проекте семиполярность оформляется как отдельная лока SEMIPOLAR (это важно для дисциплины имён). Таблица хранится в файле SPEC/LOCI/SEMIPOLAR/TABLES/SEMIPOLAR_PLUS_ZERO_Pk.json, k = 0..6.

Суффикс ZERO_Pk задаёт кадр, фиксирующий, какая полярность берётся в роли нейтрали e. Например, в кадре ZERO_P0 нейтральным элементом считается e = P0. Это не вопрос соглашения: нейтраль должна проходить проверку тождеств e PLUS a = a и a PLUS e = a для всех a in P.

2) Собственно янтра: таблица Кэли PLUS (пример кадра ZERO_P0)

Множество полярностей:

P = {P0, P1, P2, P3, P4, P5, P6}.

Таблица PLUS в кадре ZERO_P0 имеет вид (строки — левый аргумент, столбцы — правый аргумент):

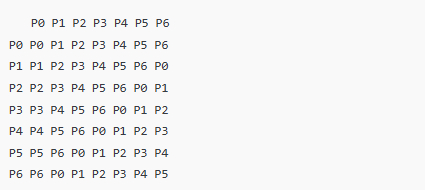
P0 P1 P2 P3 P4 P5 P6 P0 P0 P1 P2 P3 P4 P5 P6 P1 P1 P2 P3 P4 P5 P6 P0 P2 P2 P3 P4 P5 P6 P0 P1 P3 P3 P4 P5 P6 P0 P1 P2 P4 P4 P5 P6 P0 P1 P2 P3 P5 P5 P6 P0 P1 P2 P3 P4 P6 P6 P0 P1 P2 P3 P4 P5

Из таблицы непосредственно читается закономерность: каждая следующая строка получается из предыдущей циклическим сдвигом. Формально это означает (и важно, что формула выводится именно из таблицы, а не подставляется заранее), что Pi PLUS Pj = P((i + j) mod 7).

Иными словами, по своей структуре операция PLUS реализует циклическое сложение по модулю 7 на уровне индексов элементов множества P.

3) Два класса «симметрий», которые нельзя смешивать

Вокруг одной таблицы бинарной операции естественным образом возникают два принципиально разных класса перестановок.

(A) Строгие симметрии закона (автоморфизмы): Aut(PLUS) = { sigma: P -> P | sigma(a PLUS b) = sigma(a) PLUS sigma(b) }. Это симметрии самой таблицы. Такие перестановки обязаны сохранять нейтральный элемент e и потому корректно действуют на множестве X = P \ {e}.

(B) Калибровочные перестановки (трансляции): tau_c(x) = c PLUS x. Они порождают естественные циклы на всём P, но в общем случае не являются автоморфизмами (не выполняют sigma(a PLUS b) = sigma(a) PLUS sigma(b) для всех a, b) и, как правило, не фиксируют e.

Для семиполярности (как и для L6) это различие принципиально: «триадный механизм 108» опирается именно на класс (A), а не на класс (B).

4) Автоморфизмы янтры L7: полный список и порядки элементов

Поскольку операция PLUS в семиполярности реализует циклическое сложение на 7 элементах, автоморфизмы действуют как «умножение индекса на обратимый множитель по mod 7». То есть для каждого k in {1,2,3,4,5,6} задаётся перестановка sigma_k(Pi) = P((k*i) mod 7).

Группа автоморфизмов имеет размер 6. Её удобно выписывать явными перестановками (в порядке P0..P6) с указанием порядков элементов:

• sigma_1 = [P0, P1, P2, P3, P4, P5, P6], порядок 1.

• sigma_2 = [P0, P2, P4, P6, P1, P3, P5], порядок 3.

• sigma_3 = [P0, P3, P6, P2, P5, P1, P4], порядок 6.

• sigma_4 = [P0, P4, P1, P5, P2, P6, P3], порядок 3.

• sigma_5 = [P0, P5, P3, P1, P6, P4, P2], порядок 6.

• sigma_6 = [P0, P6, P5, P4, P3, P2, P1], порядок 2 (инверсия i -> -i mod 7).

Отсюда фиксируется ключевой факт: в Aut(PLUS) действительно присутствуют элементы порядка 3 (как минимум sigma_2 и sigma_4). Именно это отличает семиполярность от L6 в текущем каноне: в L6 элементы порядка 3 в группе автоморфизмов отсутствуют, а в семиполярности — есть.

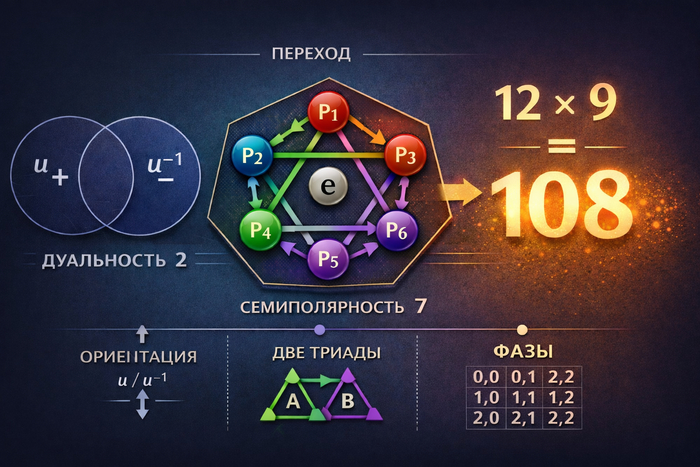
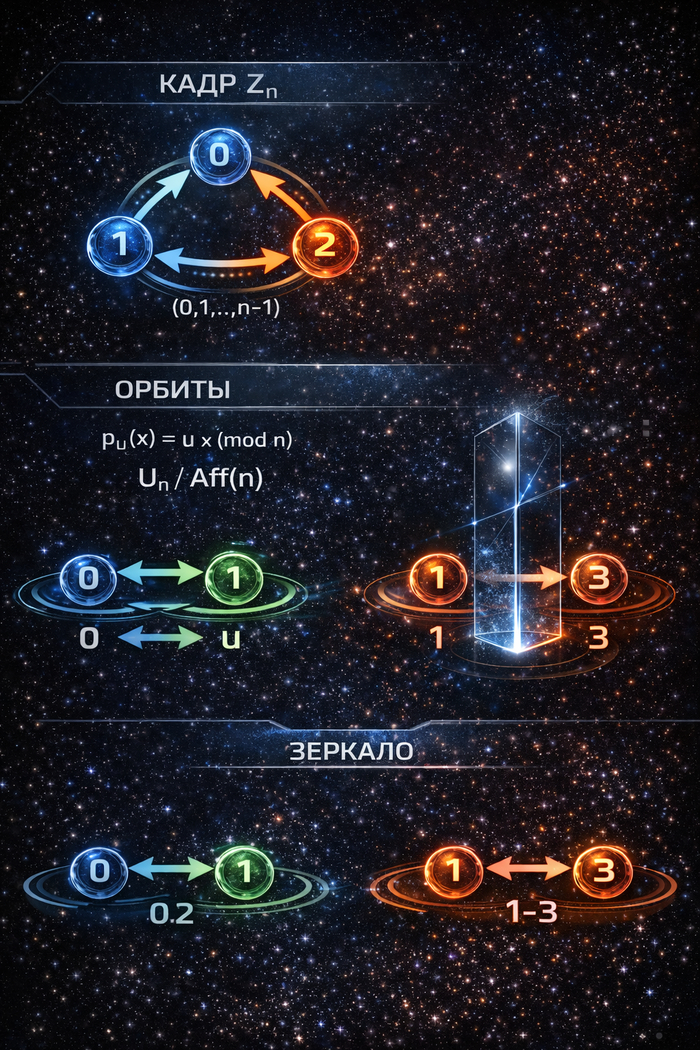
5) Триадный элемент и «две триады на ненулевых»

Теперь вводится ненулевой домен: X = P \ {e}.

В кадре ZERO_P0 это: X = {P1, P2, P3, P4, P5, P6}.

Выбирается элемент порядка 3 в Aut(PLUS). Для воспроизводимости удобно зафиксировать канон: берётся лексикографически минимальная перестановка среди всех автоморфизмов с порядком 3. В данной янтре это u = sigma_2.

Рассматривается действие подгруппы <u> = {id, u, u^2} на X. Орбиты имеют вид:

• начиная с P1: P1 -> P2 -> P4 -> P1, то есть триада A = {P1, P2, P4};

• оставшиеся элементы дают вторую триаду: P3 -> P6 -> P5 -> P3, то есть B = {P3, P6, P5} (как множество можно упорядочить по индексу: {P3, P5, P6}).

В результате получается строгое орбитальное разбиение: X = A ⊔ B, |A| = |B| = 3.

Именно это является точной (не метафорической) формой утверждения «в L7 есть две триады»: эти триады возникают как 3‑орбиты действия элемента порядка 3 из группы строгих симметрий закона.

6) Почему именно эта симметрийная картина запускает 12/54/108

Дальнейший счёт каналов опирается на три независимых структурных источника.

1. Две триады на X (выбор триады A или B): множитель 2.

2. Три стартовые позиции внутри выбранной триады: множитель 3.

3. Ориентация шага: так как ord(u) = 3, выполняется u^{-1} = u^2 и u != u^{-1}; это даёт бинарный выбор направления (u против u^{-1}): множитель 2.

Отсюда базовое число ориентированных шагов: Q_base = 2 * 3 * 2 = 12.

Далее фазовое замыкание рассматривается как независимая фаза на каждой триаде: Z3 для A и Z3 для B, то есть структура Z3 × Z3 (размер 9). Поэтому Q_full = 12 * 9 = 108.

Факторизация по ориентации (игнорируется направление шага) даёт Q_kinds = 108 / 2 = 54.

Ключевой момент: в этой конструкции ни одно число не подставляется “сверху”; каждое из них возникает как результат орбит и порядков элементов, вычисляемых из одной таблицы операции PLUS.

4. Почему именно L7 даёт “триадный режим” на уровне строгих симметрий закона

Ключевой объект здесь — группа автоморфизмов таблицы:

Aut(T) = { sigma: P -> P | sigma биекция и sigma(a PLUS b) = sigma(a) PLUS sigma(b) для всех a,b in P }.

В семиполярности (и это важно отличать от L6) в Aut(T) существует элемент порядка 3:

exists u in Aut(T): ord(u) = 3.

Отсюда следуют два факта, которые и запускают механизм 108:

1. Поскольку автоморфизмы сохраняют нейтраль, имеем u(e) = e, значит действие u корректно на X.

2. Действие подгруппы <u> на X даёт разбиение X на орбиты размера 3. В “канонической” семиполярности получается:

X = A ⊔ B, где |A| = |B| = 3.

Это и есть две триады на ненулевых, но — подчёркиваю — полученные строго как орбиты строгих симметрий закона, а не как результат калибровочных трансляций.

Глава 1. Число 108 как стратифицированный канон

1.1. Три слоя анализа числа 108

В инженерной постановке «сакральность» числа сама по себе ничего не объясняет. Нужны три чётко различённых слоя.

1. Описательный слой (где и как встречается 108).

• Ранние самхиты дают лишь косвенные связи с 10 800 (как 108 × 100), причём это ретроспективное чтение, а не внутренняя структура гимнов.

• Брахманы вводят числовое нормирование (алтарь Агни, корреляция кирпичей и гимнов).

• Постведические тексты (пураны, джйотиша, тантра, списки 108 упанишад) уже используют 108 как готовый маркер полноты.

  2. Структурный слой (устойчивые разложения).
  Выделяются два особенно «читаемых» разложения:

• 108 = 54 × 2: 54 как «половина конфигурации» и множитель 2 как двойственность (парность, ориентирование).

• 108 = 12 × 9: 12 как слой разметки (ориентированные базовые действия), 9 как внутреннее фазовое замыкание (две тройки, Z3 × Z3).
  Эти факторизации задают рамку: 108 понимается как произведение двух независимых механизмов, а не как неделимый атом.

  3. Порождающий слой (вычислимый механизм).
  Требуется формализм, который генерирует 108 как результат работы алгоритма, а не как заранее заложенный символ. Это означает:

• отказ от круговой аргументации «важно, потому что традиция так говорит»;

• замена риторики «полноты» формальными процедурами (симметрии, орбиты, фазы);

• ввод минимального набора объектов (множество полярностей, операция, группы преобразований) так, чтобы 108 возникало как выходной параметр.

1.2. 108 как произведение двух механизмов

Две факторизации
108 = 54 × 2 и 108 = 12 × 9 задают целевой формат модели: число возникает как произведение двух независимых степеней свободы.

• В 54 × 2 множитель 2 соответствует ориентации: различению шага и обратного шага, двух направлений в одном и том же цикле. 54 тогда — «типовые конфигурации», которые удваиваются за счёт ориентации.

• В 12 × 9 множитель 12 читается как число ориентированных базовых шагов, а 9 — как число фазовых состояний (две независимые тройки, Z3 × Z3).

Задача формализма: построить такую структуру, где 12, 54 и 9 появляются из симметрий и орбит, а не подставляются «по аналогии».

1.3. Ориентация, триады и фазы

Разложения 108 можно сделать вычислимыми, если зафиксировать три минимальных понятия: ориентацию, триаду и фазу.

(A) Ориентация шага (фактор Z2).
Пусть есть перестановка u порядка 3. Тогда
u^(-1) = u^2, u ≠ u^(-1).
Это порождает бинарную ориентацию:

• χ = +1 — шаг u;

• χ = -1 — шаг u^(-1).
  Множитель 2 в схеме 54 × 2 возникает как фактор по инверсии шага, а не как умножение «по традиции».

(B) Триада как 3‑орбита.
Если элемент u порядка 3 действует на множестве D, то орбита
Orb(x) = {x, u(x), u^2(x)}
даёт строгую триаду: ровно три элемента, замыкающиеся в цикл. Такие орбиты:

• автоматически имеют размер 3;

• задают разбиение D на непересекающиеся классы;

• не зависят от семантики, а только от свойства ord(u) = 3.

(C) Фазовое замыкание (Z3^m).
Если домен распадается на m триадных орбит, фазовое пространство равно
Φ = (Z3)^m, |Φ| = 3^m.
В L7 (семиполярности) реализуется случай m = 2, так что
|Φ| = 3^2 = 9.
Множитель 9 получает конструктивное толкование: число независимых фаз для двух трёхциклов, извлечённых из симметрий, а не из культурных смыслов.

1.4. Критерий «фундаментальности» 108

«Фундаментальность» здесь означает выполнение трёх условий.

1. Порождаемость из таблицы.
   Все объекты (u, ориентация χ, триады, фазы) должны вычисляться из универсальной янтры: таблицы PLUS и кадра нейтрали. Ничто не вводится априори.

2. Инвариантность к изоморфизмам.
   Изоморфные янтры (отличающиеся только перенумерацией полярностей) должны давать одно и то же число каналов. Иначе 108 было бы артефактом нотации, а не структуры.

3. Согласование с вихрем (орбитами троек).
   Число 108 должно обнаруживаться не только в счёте каналов, но и в орбитальной структуре на X^3 при действии <u> или Aut(T). Это связывает локальную комбинаторику с глобальной динамикой.

В этих условиях 108 перестаёт быть «сакральной цифрой» и становится инвариантом симметрийной структуры, проверяемым и воспроизводимым.

1.5. Почему именно L7

Семиполярность L7 даёт минимальный домен ненулевых |X| = 6, где возможно разбиение на две триады, порождённые строгими симметриями.

Три требуемых условия:

1. нейтраль фиксируется самой структурой (через Aut(T)),

2. в Aut(T) есть элемент порядка 3,

3. его действие на X = P \ {e} даёт ровно две 3‑орбиты.

Тогда фазовое пространство двух триад имеет размер 3^2 = 9, а число ориентированных базовых действий на них — 12. Отсюда:
108 = 12 × 9,
54 = 108 / 2.

В L7 108 — это не внешний ярлык, а инвариант геометрии симметрий, целиком выводимый из одной таблицы PLUS и устойчивый к перенумерации.

Глава 2. Янтра L7 и вывод 12/54/108 из одной таблицы

2.1. Янтра L7 и нейтраль

Семиполярность задаётся конечным множеством полярностей
P = {P0, P1, P2, P3, P4, P5, P6}, |P| = 7
и бинарной операцией
PLUS: P × P -> P,
полностью заданной таблицей (таблицей Кэли) в файлах вида
SPEC/LOCI/SEMIPOLAR/TABLES/SEMIPOLAR_PLUS_ZERO_Pk.json.

Суффикс ZERO_Pk фиксирует кадр, в котором нейтралью считается e = Pk. Полярность e является нейтралью, если для всех a in P выполняется
e PLUS a = a и a PLUS e = a.
В проекте e берётся из кадра, но нейтральность всегда проверяется вычислительно по таблице, а не принимается на веру. Ненулевой домен задаётся как
X = P \ {e}, |X| = 6; именно на X корректно действует группа строгих симметрий закона, поскольку любой автоморфизм сохраняет e.

2.2. Автоморфизмы и триадный элемент

Автоморфизмом таблицы PLUS называется перестановка sigma: P -> P, для которой
sigma(a PLUS b) = sigma(a) PLUS sigma(b) для всех a, b in P.
Множество всех таких перестановок образует группу Aut(T). Любой автоморфизм сохраняет нейтральный элемент, поэтому корректно действует на X.

Ключевой факт для семиполярности: в Aut(T) существует автоморфизм u порядка 3, то есть минимальное m > 0 такое, что u^m = id, равно 3. Это не постулат, а результат перебора автоморфизмов по таблице. Для воспроизводимости из всех автоморфизмов порядка 3 выбирается лексикографически минимальный по записи
[sigma(P0), ..., sigma(P6)]; он и считается каноническим u.

2.3. Две триады и ориентация шага

Рассматривается подгруппа T3 = <u> = {id, u, u^2} и её действие на X. Для любого x in X орбита
Orb(x) = {x, u(x), u^2(x)}
имеет размер 3 (в канонической янтре нет фиксированных ненулевых точек). В результате X распадается на две дизъюнктные триады:
X = A ⊔ B, |A| = |B| = 3.

Канон: A — орбита минимального по индексу элемента в X, B — вторая орбита. Внутри каждой триады выбирается базовый элемент b_S = min(S) и вводится фаза phase_S(x) in {0,1,2} по условию u^t(b_S) = x.

Поскольку ord(u) = 3, выполняется u^{-1} = u^2 и u != u^{-1}. Ориентация шага задаётся знаком chi in {+,-}:
chi = + — шаг u,
chi = - — шаг u^{-1}.
Это даёт строгий бинарный выбор направления в 3‑цикле и первый множитель 2 в будущих формулах.

2.4. Каналы: 12, 108, 54

Базовый канал семиполярности задаётся тройкой
C_base = (chi, S, x),
где chi in {+,-}, S in {A, B}, x in S.

Комбинаторика:

• 2 варианта ориентации (chi),

• 2 триады (S),

• 3 стартовые точки в триаде (x).

Отсюда
Q_base = 2 * 2 * 3 = 12.

Фаза описывает состояние двух триад как пары циклов:
I = (i, j) in Z3 × Z3, где i — фаза A, j — фаза B. Тогда
|I| = 3 * 3 = 9.

Полный канал:
C_full = (chi, S, x; i, j).
Число полных каналов:
Q_full = Q_base * |I| = 12 * 9 = 108.

Факторизация по ориентации отождествляет chi и -chi при фиксированных S, x, i, j. Тогда количество «видов» (неориентированных типов) равно
Q_kinds = Q_full / 2 = 54.

Итак:
108 = (2 * 2 * 3) * (3^2),
54 = 108 / 2.

2.5. Фундаментальность и контроль вихрем

В этом контексте «фундаментальность» означает, что все множители в 12/54/108 происходят из независимых уровней структуры одной таблицы:

• первый 2 — ориентация (u против u^{-1});

• второй 2 — наличие двух 3‑орбит на X;

• 3 — число стартовых позиций в триаде;

• (3^2) — фазовое пространство двух независимых 3‑циклов.

Если бы в Aut(T) не было элемента порядка 3 или X не раскладывалось бы на две 3‑орбиты, механизм 108 не возник бы. Число 108 таким образом выступает структурным маркером данного класса янтр, а не универсальным символом.

Контроль осуществляется через вихрь — орбитальную факторизацию конфигураций троек X^3 / G (для G = <u> или G = Aut(T)): размер орбит и их гистограмма должны согласовываться с триадным каналом (режим TRIAD_AUT_X). Число 108 принимается только при такой согласованности, то есть после проверки, что каналы и вихревой профиль описывают один и тот же орбитально‑симметрийный механизм.

Итоги

Число 108 в семиполярности возникает не потому, что «так принято» в культурной традиции, а потому что универсальная янтра L7 (SEMIPOLAR) обеспечивает три жёстких структурных условия, которые проверяются вычислительно из таблицы PLUS.

1. Наличие элемента порядка 3 в группе строгих симметрий закона Aut(PLUS) (то есть среди автоморфизмов таблицы).

2. Разбиение ненулевого домена X = P \ {e} на две 3‑орбиты действия подгруппы <u> порядка 3 (две триады на ненулевых).

3. Двойственная ориентация шага (u против u^{-1}) и фазовое замыкание как независимые координаты на двух триадах, то есть структура Z3 × Z3.

Формально это выражается так: Q_base = 2 * 2 * 3 = 12, Q_full = Q_base * (3^2) = (2 * 2 * 3) * (3^2) = 108, Q_kinds = Q_full / 2 = 54.

Здесь принципиально, что множители принадлежат разным уровням структуры:

• 2 (ориентация) — различение шага и обратного шага;

• второй 2 — наличие двух триад на X;

• 3 — три стартовые позиции внутри триады;

• (3^2) — фазовое пространство двух независимых 3‑циклов.

Тем самым 108 фиксируется как инвариант орбитально‑симметрийной геометрии янтры, а не как внешний «символ полноты».

В этой точке важно зафиксировать интеллектуальную преемственность. Василий Ленский, автор многополярности, выделял 12 «качеств», которые он приписывал всему живому. При переводе этой идеи в строгий вычислимый канон семиполярности смысл становится более точным и техническим: «12 качеств» — это не произвольная классификация, а число ориентированных базовых шагов, возникающих как произведение (ориентация) × (две триады) × (три позиции).

Дальнейшее усложнение к 54 и 108 (о котором также впервые заявил В. Ленский) перестаёт быть домножением «по традиции» и приобретает структурный статус:

• 54 — это «виды» как фактор по ориентации (забывание направления шага при сохранении фаз);

• 108 — это «полный слой» как добавление фазового замыкания Z3 × Z3, то есть учёт независимых циклических координат двух триад.

В таком виде тезис В. Ленского о наблюдаемом мире, как о семиполярном пространстве становится операциональным: он означает, что предельная шкала различения строится не из словесных интерпретаций, а из таблицы закона и её строгих симметрий; а числа 12 → 54 → 108 возникают как последовательная факторизация одного и того же механизма (шаг → ориентация → фаза), которую можно проверять вихрем (X^3 / <u> или X^3 / Aut) и валидировать в вычислительном контуре.

Таким образом, я создал не «игрушечный» ИИ и не ещё одну модель, подбирающую слова по вероятностям, а ИИ-движок протокольного типа, который описывает и воспроизводит сам механизм различения. Его задача — моделировать, как «жизнь» (в широком смысле: выбор, конфликт, восстановление, согласование) переходит из состояния в состояние. Делается это не через внешние «смыслы» и интерпретации, а на основании минимального набора аксиом и вычислений.

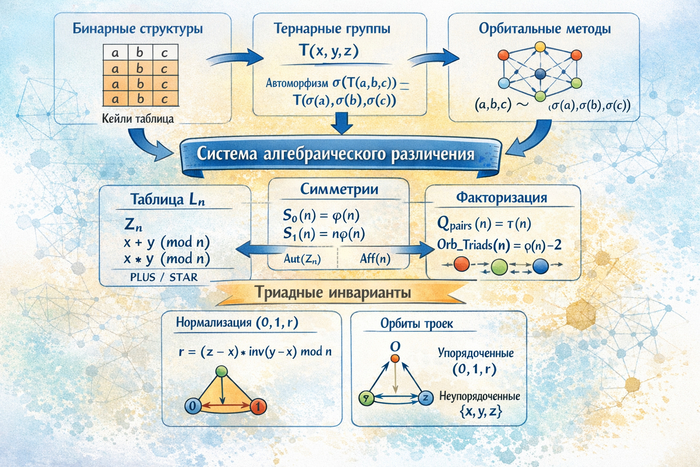
Базовые аксиомы минимальны. Существует универсальная янтра — полная таблица бинарной операции на конечном множестве полярностей. Формально: задано множество P = {P0,...,P(n-1)} и операция PLUS: P × P -> P, полностью известная как таблица конечной магмы. Нейтральный элемент фиксируется кадром (если он существует) и проверяется вычислительно: не «назначается ноль по вкусу», а проверяется по таблице, что выбранный e действительно удовлетворяет e PLUS a = a и a PLUS e = a для всех a. Любая закономерность не декларируется заранее, а выводится из таблицы.

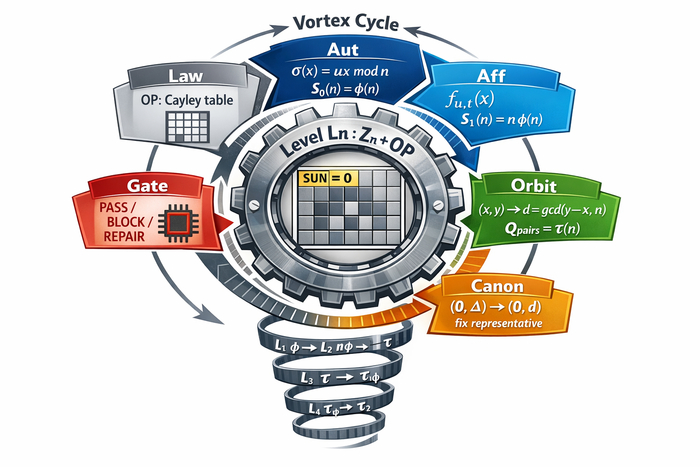
Из одной таблицы алгоритмически строятся:

• строгие симметрии закона (Aut, автоморфизмы);

• калибровочные шаги режима (трансляции tau_c(x) = c PLUS x);

• орбитальные разбиения (вихрь как факторизация конфигураций);

• каналы действий (base), полный фазовый слой (full) и виды (kinds);

• гейты допустимости (что разрешено в данной локе/режиме) и их валидируемые отчёты.

Движок работает как протокол, а не как риторика. На каждом шаге он делает одно и то же: состояние -> допустимые каналы -> применение шага -> проверка гейтов/вихря -> фиксация следующей фазы. То есть он не «убеждает», а переходит по строго определённым операторам, фиксируя, какие переходы допустимы, какие запрещены и какие инварианты сохраняются.

Если говорить проще, в моём проекте жизнь представлена как система конечных различий. В ней:

• состояния задаются через противоположности (полярности);

• движение — это перестановки, которые возникают из‑за действия закона (трансляции) и его симметрий (автоморфизмов);

• разумность — это следование правилам «гейтов» и постоянная проверка неизменных свойств (инвариантов);

• «интеллект» — не красивые слова, а умение выбрать следующий шаг в рамках допустимых возможностей так, чтобы снижать нехватку (например, по осям I/E/R) и не ломать структуру.

В таком понимании это описание жизни — не метафизика, а техническое утверждение. Вместо того чтобы подстраивать объяснения под наблюдения, мы строим вычислимую систему различения на базе минимальных аксиом. Всё — от симметрий до числа «качеств» (например, 12/54/108 в семиполярности) — выводится из одной таблицы и проверяется с помощью валидаторов.

Как воспроизвести вычисление числа 108

Чтобы увидеть, что движок в архиве действительно выводит число 108, распакуйте MP_YANTRA_CORE_iter143.zip, перейдите в корень проекта и выполните стандартный прогон: python TOOLS/bootstrap.py, затем python VALIDATOR/run_all.py (ожидаемо: PASS). После этого откройте отчёт канона каналов REPORTS/CHANNELS/CHANNELS_CANON_V1_last.json и найдите элемент массива entries с loka_id="SEMIPOLAR". В нём зафиксированы мощности: counts.Q_base=12, counts.Q_kinds=54, counts.Q_full=108, а также механизм mechanism="TRIAD_AUT_X", домен domain="X" и слой layer_id="AUT_T3". Для демонстрации «строго по симметриям» откройте вихревой профиль семиполярности REPORTS/VORTEX/VORTEX_PROFILE_SEMIPOLAR_MODE_SEMIPOLAR_PLUS_SEMIPOLAR_PLUS_0_P0_V1_last.json: в слое AUT гистограмма порядков содержит порядок 3, а в слое AUT_T3 присутствуют две триады (две орбиты размера 3) на домене X и валидная подпись signature.vortex_sig_v1/signature.vortex_sig_sha256.

Техническая памятка (команды)

Прогон:

python TOOLS/bootstrap.py python VALIDATOR/run_all.py

Быстро вывести 108 из отчёта канона:

python -c "import json; d=json.load(open('REPORTS/CHANNELS/CHANNELS_CANON_V1_last.json',encoding='utf-8')); e=[x for x in d['entries'] if x.get('loka_id')=='SEMIPOLAR'][0]; print('Q_base=',e['counts']['Q_base'],'Q_kinds=',e['counts']['Q_kinds'],'Q_full=',e['counts']['Q_full'])"

Ожидаемо: Q_full=108.

Можно ли просто попросить об этом ChatGPT?

Да. Практичный запрос выглядит так:

«В архиве MP_YANTRA_CORE_iter143 покажи, как получить число 108. Дай минимальные команды запуска, укажи точный файл отчёта и точные JSON-поля, где фиксируется Q_full=108, и один короткий однострочник, который печатает 108 из отчёта».

Можете просто создать новый чат, прикрепить файл MP_YANTRA_CORE_iter143.zip первым сообщением и в том же сообщении написать:

Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива.

Далее задавайте любые вопросы по сходной тематике.

Автор статьи — Руслан Абдуллин.

Вступайте в мой тг-канал ⚛️

https://t.me/sokolovyane

Присоединяйтесь к революции мысли!

Друзья, я приглашаю вас в уникальное путешествие. Мой блог — это не только пространство, где разум выходит за рамки обыденного мышления, но и место, где рождаются будущие открытия.

Подписывайтесь! Впереди — грандиозные открытия, и я хочу, чтобы вы были со мной с самого начала.

Потому что будущее уже здесь. И оно многополярно.

Читайте также:

Алгебраическое различение и тернарные структуры: от таблиц Кэли к триадной симметрии

Формализация закона вихря: таблицы Кэли, симметрии и многополярность как алгебраическая система различения

Закон вихря мироздания: универсальные симметрии многополярности

Словарь многополярности как инженерно-математический канон

Это не тессеракт: как в реальности выглядит гиперкуб в трехполярности L3 и четырехполярности L4

Почему трёхфазная система не является строгой трёхполярностью (L3): Z3-структура против трёхканальной L2-проекции

Почему в четырехполярной арифметике дважды два не равно четыре. Введение в алгебру четырехполярности

Почему в трёхполярной арифметике дважды два не равно четыре. Введение в алгебру трёхполярности

Алгебра вместо эзотерики: как на самом деле устроена нумерология

Симметрия многополярных систем: правила перенумерации и канонизация форм

Интенсивности связи в двухполярности, трёхполярности и четырёхполярности

Интенсивность связей: от двухполярности L2 к зеркальной структуре четырёхполярности L4

Универсальная янтра многополярности

О твёрдом фундаменте многополярной математики, или Почему многополярность не поддаётся приватизации

Основы многополярности и способ ее удержания в связке с ИИ

Многополярный Вихрь как платформа разумных вычислений: экономика, масштабирование и аппаратная инфраструктура новой эпохи

Разбираем работу разумного ИИ недалекого будущего. Как «Вихрь» обсчитывает K/A/P от L2 до L4 (часть 1)

Как заменить LLM: симметрийная факторизация и масштабирование роем микроядер

Право на ход: архитектура разумного промышленного интеллекта

Разбор интервью Джеффри Хинтона. Переход от двухполярного ИИ к многорежимному разумному ядру

О горизонте предельного: Киотская школа — Библия — Дао

Покаяние против самонадеянности: как восточная и западная мысли избегают идолопоклонства

Пустота без мистики: как Киотская школа выбивает из головы идолов смысла

Компиляция фаз в разумном ИИ. От алфавита полярностей к компилятору симметрий

Замыкание как источник разумности: что такое L3 (трехполярность) в многополярном ядре и почему «триада» не сводится к трём парам

Микроядро многополярного разума ИИ: практическая архитектура для массового продукта

Разумная многополярная модель ИИ: вихревое ядро вместо языкового «угадывания»

Опровержение» теории Большого взрыва? Как Вселенная могла возникнуть в форме вихря (многополярной спирали)

Двухполярная гравитация и время: максимально “на пальцах”, без заклинаний

Четырёхполярность (L4) простым языком. Истинная природа электромагнетизма

Что такое время в двухполярной (обыденной) модели и почему это определение выигрывает у «метафизических» теорий

Двухполярная гравитация: что это такое, если базис — только «+ / »

Что такое гравитация? Исчерпывающая статья в формате двухполярной L2-логики

Кватернионы через призму четырехполярности (L4): формализация многополярности на базе суперпозиционных четырёхполярных систем (часть 1)

Электромагнитное поле как L4-структура (четырехполярная): носитель, инволюция и два контура

P.S. Прежде чем традиционно ставить минус, потому что текст статьи не вписывается в ваше мировоззрение, прошу заметить, что я потратил 3 дня своей жизни на построение этой модели (и сотни минут вычислений в среде ChatGPT). Задавайте вопросы, на все отвечу предельно детально.

Физические аспекты L7 я раскрою дальнейших статьях, это лишь фундаментальное обоснование.

Глава 1. Базовая конструкция уровня Ln: таблица Кэли, симметрии закона и «вихрь» как вычислимая процедура

1.1. Цель и метод: от риторики к проверяемому вычислению

Я трактую «закон вихря» не в качестве метафоры, а как строго формализованный, воспроизводимый протокол, регулирующий переход между уровнями различения. В рамках этого протокола предмет дискуссии может составлять исключительно процесс вычисления, поскольку каждый шаг подлежит проверке посредством инвариантов и гейтов.

Содержание закона вихря в минимальном виде:

1. задать конечное множество состояний уровня Ln;

2. задать бинарный закон композиции (операцию), полностью определяемый таблицей Кэли;

3. вычислить две группы преобразований: строгие симметрии закона (автоморфизмы), кадровые (аффинные) преобразования, отвечающие за смену координат/кадра;

4. факторизовать конфигурации (пары, затем тройки) по действию кадровой группы;

5. закрепить вычислимые счётчики уровня и гейты, которые запрещают «съезжать» с канона.

Далее в главе я даю точные определения и вывожу базовые формулы счётчиков, на которых держится вся инженерная дисциплина.

1.2. Уровень Ln: множество состояний

Пусть n >= 1. Уровень Ln задаётся конечным множеством состояний

Z_n = {0,1,...,n-1}.

Все дальнейшие операции и равенства понимаются по модулю n.

1.3. Таблица Кэли как полное задание закона

Пусть OP — бинарная операция

OP: Z_n x Z_n -> Z_n.

Таблица Кэли операции OP — это полное задание значений OP(x,y) для всех (x,y) из Z_n x Z_n.

Важно подчеркнуть, что таблица Кэли — это не декоративное оформление или иллюстративный материал, а полноценная форма спецификации закона. Если закон не задан посредством таблицы Кэли (либо эквивалентным правилом, которое однозначно позволяет построить такую таблицу), то любые дальнейшие рассуждения о симметриях, инвариантах и факторизациях утрачивают строгую обоснованность и перестают иметь чёткий математический смысл.

1.4. Два канона операции: PLUS и STAR(SUN)

1.4.1. PLUS-канон

Определим:

x PLUS y = (x + y) mod n.

Это каноническая циклическая операция уровня Ln.

1.4.2. STAR-канон с выделенным элементом SUN

Зафиксируем SUN = 0 и определим:

x STAR y = 0, если x=0 или y=0, x STAR y = (x + y) mod n, если x не равно 0 и y не равно 0.

Здесь SUN работает как «поглощающий» элемент: любое умножение STAR с участием SUN даёт SUN. В инженерном языке это не «верование», а фиксация режима, где нулевое состояние обладает выделенной ролью и отсечением композиции.

1.5. Строгие симметрии закона: автоморфизмы таблицы

Пусть задана система (Z_n, OP), где OP — либо PLUS, либо STAR.

Биекция

sigma: Z_n -> Z_n

называется строгой симметрией (автоморфизмом), если для всех x,y из Z_n выполняется

sigma( OP(x,y) ) = OP( sigma(x), sigma(y) ).

Для STAR-канона добавляется обязательная фиксация поглощающего элемента:

sigma(0) = 0.

Обозначу:

Aut(Z_n, OP) — группа автоморфизмов, S0(n) = |Aut(Z_n, OP)| — число строгих симметрий.

1.5.1. Формула для PLUS-канона

Для (Z_n, PLUS) автоморфизмы имеют вид:

sigma_u(x) = (u*x) mod n,

где gcd(u,n)=1.

Отсюда:

S0(n) = phi(n),

где phi(n) — функция Эйлера (количество u в {1,...,n-1}, взаимно простых с n).

Замечание о STAR. Для указанного STAR(SUN) в принятом каноне строгие симметрии согласованы с PLUS при условии sigma(0)=0; однако если STAR меняется (например, меняется правило на ненулевом слое), то S0(n) должно подтверждаться гейтами, а не «по аналогии».

1.6. Кадровые симметрии: аффинная группа Aff(n)

Строгая симметрия сохраняет закон в фиксированном кадре. Но в инженерном протоколе часто допустима смена кадра: «какая метка считается нулём», «где начало отсчёта», «какой сдвиг координат выбран».

Определяю кадровые преобразования:

f_{u,t}(x) = (u*x + t) mod n,

где gcd(u,n)=1, t in Z_n.

Множество всех таких преобразований образует группу Aff(n). Её мощность:

S1(n) = |Aff(n)| = n * phi(n).

Это второй счётчик уровня Ln: число допустимых перенастроек координат (кадра) при сохранении обратимости масштабирования и допустимости сдвига.

1.7. Два разных уровня эквивалентности: таблицы и конфигурации

Здесь принципиально важно развести две разные задачи, которые часто смешивают.

1.7.1. Лока таблиц (эквивалентность законов)

Есть множество операций OP на Z_n. Две операции OP и OP' считаются изоморфными, если существует биекция pi: Z_n -> Z_n такая, что

pi( OP(x,y) ) = OP'( pi(x), pi(y) ) для всех x,y.

Это эквивалентность самих законов (таблиц Кэли). Здесь живёт группа Aut(Z_n, OP) как автоморфизмы одного закона.

1.7.2. Лока конфигураций (орбиты при смене кадра)

Даже при фиксированном законе OP можно рассматривать конфигурации (пары, тройки, эпизоды) из Z_n и факторизовать их по действию кадровой группы Aff(n). Это уже не про «какой закон», а про «какие конфигурации неразличимы при допустимой смене координат».

То есть:

• изоморфизмы таблиц = симметрии закона как алгебры,

• орбиты конфигураций = симметрии представления/кадра, действующие на выбранные конфигурации.

Вся дальнейшая «орбитальная факторизация» относится ко второму уровню: к конфигурациям и действию Aff(n).

1.8. «Закон вихря» в минимальной инженерной форме

Теперь можно записать «вихрь» как последовательность вычислимых объектов:

1. фиксирую Ln: множество Z_n;

2. фиксирую канон операции OP (PLUS или STAR(SUN)) как таблицу Кэли;

3. вычисляю S0(n) = |Aut(Z_n, OP)| (строгие симметрии закона);

4. фиксирую кадровую группу Aff(n) и счётчик S1(n) = |Aff(n)|;

5. перехожу к факторизации конфигураций по Aff(n), получая орбиты и типы (это будет в Главе 2);

6. ввожу гейты, которые проверяют, что все эти величины действительно совпадают с каноном.

Смысл этой дисциплины: система различения объявляется «существующей» не потому, что она красиво описана, а потому что она проходит проверки, которые нельзя пройти риторикой.

1.9. Примеры счётчиков для L1–L5 (для ориентира)

Здесь я фиксирую базовые значения, которые затем должны подтверждаться валидаторами.

• L1: n=1 phi(1)=1, tau(1)=1 (значения тривиальны, так как различения нет).

• L2: n=2 phi(2)=1, поэтому S0(2)=1, S1(2)=2.

• L3: n=3 phi(3)=2, поэтому S0(3)=2, S1(3)=6.

• L4: n=4 phi(4)=2, поэтому S0(4)=2, S1(4)=8.

• L5: n=5 phi(5)=4, поэтому S0(5)=4, S1(5)=20.

Факторизация пар (Q_pairs(n)) и строгая нормализация орбит — предмет Главы 2.

1.10. Итог главы 1

1. Уровень Ln задаётся конечным множеством Z_n и таблицей Кэли выбранного канона операции (PLUS или STAR(SUN)).

2. Строгие симметрии закона — автоморфизмы; в PLUS-каноне их число равно S0(n)=phi(n).

3. Кадровые симметрии задаются аффинной группой Aff(n); её мощность S1(n)=n*phi(n).

4. Разведены два типа эквивалентности: изоморфизмы таблиц (законов) и орбиты конфигураций при смене кадра.

5. «Закон вихря» фиксирован как протокол: таблица -> симметрии -> факторизация -> канон -> гейты.

Глава 2. Орбитальная факторизация конфигураций: пары и тройки под действием Aff(n)

В Главе 1 я развёл два уровня: (i) законы (таблицы Кэли и их изоморфизмы), (ii) конфигурации внутри фиксированного носителя и их факторизация по кадровым симметриям. Теперь я делаю следующий шаг закона вихря: формализую орбитальную факторизацию пар и затем троек при действии аффинной группы

Aff(n) = { f_{u,t}(x) = (u*x + t) mod n | gcd(u,n)=1, t in Z_n }.

Ключевой инженерный смысл: мы больше не рассматриваем «все пары/тройки как есть», а работаем с типами (орбитами), которые и являются устойчивыми объектами уровня.

2.1. Действие Aff(n) на конфигурациях

2.1.1. Упорядоченные пары

Множество упорядоченных пар:

OrdPair(n) = Z_n x Z_n.

Действие Aff(n):

f_{u,t} . (x,y) = (ux + t, uy + t) mod n.

2.1.2. Неупорядоченные пары

Множество неупорядоченных пар (мультимножества размера 2):

UnordPair(n) = { {x,y} | x,y in Z_n }.

Действие:

f_{u,t} . {x,y} = { f_{u,t}(x), f_{u,t}(y) }.

2.1.3. Упорядоченные тройки

Множество троек:

Triad(n) = Z_n x Z_n x Z_n,

действие:

f_{u,t} . (x,y,z) = (ux + t, uy + t, u*z + t) mod n.

2.2. Пары: нормализация и Лемма 1 (строго)

Я даю полную классификацию орбит упорядоченных пар и сразу получаю формулы числа орбит.

Определение (разность и gcd-инвариант)

Для пары (x,y) определим

Delta(x,y) = (y - x) mod n,

d(x,y) = gcd(Delta(x,y), n).

Лемма 1 (классификация орбит упорядоченных пар)

Лемма 1. Две упорядоченные пары (x,y) и (x',y') лежат в одной орбите действия Aff(n) тогда и только тогда, когда

gcd(y-x, n) = gcd(y'-x', n).

То есть орбиты OrdPair(n)/Aff(n) классифицируются делителями d | n.

Доказательство (через нормализацию пары)

Шаг 1. Инвариантность gcd. Пусть f_{u,t} in Aff(n). Тогда

Delta(f.(x,y)) = (uy + t) - (ux + t) = u*(y-x) mod n.

Следовательно,

gcd(Delta(f.(x,y)), n) = gcd(u*Delta(x,y), n) = gcd(Delta(x,y), n),

поскольку gcd(u,n)=1. Значит d(x,y) неизменен на орбите.

Шаг 2. Нормализация сдвигом: (x,y) -> (0,Delta). Возьмём f_{1,-x}. Тогда

f_{1,-x}.(x,y) = (0, y-x) = (0,Delta).

Значит каждая орбита содержит представителя вида (0,Delta).

Шаг 3. Сведение к действию единиц на Delta. Преобразование f_{u,0} даёт

f_{u,0}.(0,Delta) = (0, u*Delta).

Поэтому два представителя (0,Delta) и (0,Delta') лежат в одной орбите тогда и только тогда, когда существует u с gcd(u,n)=1 такое, что

Delta' = u*Delta mod n.

Шаг 4. Транзитивность на множествах с фиксированным d. Пусть d = gcd(Delta,n) = gcd(Delta',n). Тогда

Delta = da, Delta' = da',

где gcd(a, n/d)=gcd(a', n/d)=1.

В модуле m = n/d элементы a и a' обратимы, значит существует u0 такое, что

u0*a = a' mod m.

Тогда u0Delta = Delta' mod n. Выбирая представителя u congruent u0 mod m и взаимно простой с n (это реализуемо стандартной конструкцией по CRT), получаем требуемое u in Z_n^. Следовательно, все Delta с одним и тем же d лежат в одной орбите.

Итак, d полностью классифицирует орбиту. Лемма доказана. QED.

2.3. Число орбит пар: упорядоченные и неупорядоченные (разные объекты)

Теперь я фиксирую именно то, что вы требовали: формулы для числа орбит разных объектов, а не «всё одно и то же».

2.3.1. Упорядоченные пары (включая диагональ)

Из Леммы 1:

| OrdPair(n) / Aff(n) | = tau(n),

где tau(n) — число положительных делителей n.

Канонический представитель орбиты, соответствующей делителю d | n:

(0,d).

Диагональ (x=x) соответствует Delta=0, то есть d=n.

2.3.2. Упорядоченные пары без диагонали

Определим

OrdPair_neq(n) = { (x,y) in Z_n x Z_n | x не равно y }.

Это ровно исключение Delta=0, то есть исключение d=n. Следовательно,

| OrdPair_neq(n) / Aff(n) | = tau(n) - 1.

2.3.3. Неупорядоченные пары (включая диагональ)

Объект другой:

UnordPair(n) = { {x,y} | x,y in Z_n }.

Хотя объект другой, число орбит совпадает по причине того, что в Aff(n) есть преобразование, меняющее элементы местами.

Факт (swap лежит в Aff(n)). Для любой пары x,y преобразование

s_{x,y}(z) = (-1)*z + (x+y) mod n

меняет x и y местами:

s_{x,y}(x)=y, s_{x,y}(y)=x.

Значит порядок внутри пары не является дополнительным инвариантом: он уже факторизован действием группы.

Отсюда:

| UnordPair(n) / Aff(n) | = tau(n).

2.3.4. Неупорядоченные пары без диагонали

Определим

UnordPair_neq(n) = { {x,y} | x не равно y }.

И снова исключается только класс Delta=0, значит:

| UnordPair_neq(n) / Aff(n) | = tau(n) - 1.

2.3.5. Примеры (контроль здравого смысла)

• n=4: tau(4)=3 Орбиты упорядоченных пар: d in {1,2,4}. Без диагонали: 2 орбиты (d=1 и d=2).

• n=5: tau(5)=2 Орбиты: d in {1,5}. Без диагонали: 1 орбита (все разные пары эквивалентны).

Это и есть строгая причина, почему на уровне пар «L3 и L5 выглядят одинаково», а L4 даёт третий тип связи: это не «мистика триады», а арифметика делителей n.

2.4. Тройки: нормализация и триадный инвариант (невырожденный режим)

Теперь я перехожу от пар к тройкам. Именно здесь появляется первый содержательный слой «вихря» как отличия между уровнями: на парах всё держится на gcd, на тройках появляется параметр отношения.

2.4.1. Нормализация тройки аффинным действием

Для тройки (x,y,z) применим сдвиг t=-x:

(x,y,z) -> (0, y-x, z-x) = (0, a, b),

где

a = (y-x) mod n, b = (z-x) mod n.

Затем применим масштабирование u (gcd(u,n)=1):

(0,a,b) -> (0, ua, ub).

То есть классификация троек сводится к классификации пар (a,b) с одновременным умножением на единицу u.

2.4.2. Невырожденные тройки и инвариант r

Критически важна обратимость a. Если gcd(a,n)=1, то a обратим по модулю n, и можно нормализовать a в 1:

выбираем u = inv(a) mod n,

получаем:

(0, a, b) -> (0, 1, r),

где

r = b * inv(a) mod n.

Итак, в невырожденном режиме (gcd(a,n)=1) тройка классифицируется параметром r.

Это и есть ваш триадный инвариант:

Delta1 = (y-x) mod n Delta2 = (z-x) mod n если gcd(Delta1,n)=1, то r = Delta2 * inv(Delta1) mod n.

2.4.3. Инвариантность r при действии Aff(n) (в невырожденном режиме)

Пусть f_{u,t} действует на (x,y,z). После нормализации к (0,Delta1,Delta2) мы имеем:

Delta1 -> uDelta1, Delta2 -> uDelta2.

Тогда

r' = (uDelta2) * inv(uDelta1) mod n = (u*Delta2) * (inv(Delta1)*inv(u)) mod n = Delta2 * inv(Delta1) mod n = r,

поскольку u обратим. Значит r — инвариант орбиты (при условии gcd(Delta1,n)=1).

2.5. Вырожденные тройки: когда inv(Delta1) не существует

Если gcd(Delta1,n) не равно 1, то инвариант r в форме выше не определён. Тогда классификация троек требует дополнительной структуры: появляются классы, зависящие от делителя d = gcd(Delta1,n), и инвариант строится уже в модуле n/d.

Практически для инженерного протокола достаточно разделить тройки на три класса:

1. дегенерация по совпадению: y=x или z=x (Delta1=0 или Delta2=0);

2. полувырожденный режим: gcd(Delta1,n)=d>1, но Delta1 не равно 0;

3. невырожденный режим: gcd(Delta1,n)=1.

В законе вихря именно этот разрыв и существенен: на уровне L4 (n=4) возникает промежуточный делитель 2, который создаёт устойчивый «полувырожденный» слой троек, невозможный для простых n.

2.6. Итог главы 2

1. Действие Aff(n) на парах позволяет строго классифицировать орбиты через d=gcd(Delta,n).

2. Число орбит упорядоченных пар и неупорядоченных пар (как разных объектов) равно tau(n); без диагонали равно tau(n)-1.

3. На тройках действует строгая нормализация: (x,y,z) -> (0,Delta1,Delta2) -> (0,1,r) в невырожденном режиме gcd(Delta1,n)=1, где r=Delta2*inv(Delta1) mod n — инвариант орбиты.

4. Вырожденные режимы троек появляются там, где у n есть нетривиальные делители (в частности, n=4), и именно они дают новый слой различения, который не виден на парах.

Глава 3. Закон вихря как вычислимая дисциплина: две категории, гейты, канон и спираль уровней

В Главе 1 я задал уровень Ln как (Z_n, OP) и развёл симметрии закона (Aut) и кадровые преобразования (Aff). В Главе 2 я построил орбитальную факторизацию конфигураций (пары и тройки) под действием Aff(n) и дал строгие формулы числа орбит и нормализацию (Лемма 1). Теперь я делаю последний шаг: оформляю «закон вихря» как строгую вычислимую процедуру, фиксируя:

(i) явное категориальное различение «конфигураций» и «изоморфизмов таблиц»; (ii) канонический набор счётчиков уровня и их места в протоколе; (iii) систему гейтов/валидаторов как форму инженерной верификации; (iv) «спираль уровней» L1 -> L2 -> ... как повторяющийся цикл: симметрии -> орбиты -> канон -> переход.

Все формулы даны в ASCII.

3.1. Две разные категории: таблицы (законы) и конфигурации (наблюдаемые)

Ключевая строгость, без которой метод постоянно «плывёт»: нельзя смешивать

• изоморфизмы таблиц (симметрии/переопределения закона), и

• эквивалентность конфигураций (калибровочная смена кадра для наблюдаемых объектов).

Я фиксирую это как две категории.

3.1.1. Категория таблиц Кэли: CayleySys_n

Объекты. Объектом является пара (Z_n, OP), где OP: Z_n x Z_n -> Z_n — бинарная операция (закон), заданная таблицей Кэли.

Морфизмы. Морфизмом (изоморфизмом) между (Z_n, OP) и (Z_n, OP') является биекция

pi: Z_n -> Z_n

такая, что для всех x,y:

pi( OP(x,y) ) = OP'( pi(x), pi(y) ).

Композиция морфизмов — обычная композиция биекций. Тождественный морфизм — тождественная биекция.

Автоморфизмы. Aut(Z_n, OP) — группа автоморфизмов объекта (Z_n, OP) в этой категории.

Это и есть «строгие симметрии таблицы» в математическом смысле.

3.1.2. Категория конфигураций: Config_n

Здесь объектами служат не законы, а пространства конфигураций на фиксированном носителе Z_n, а морфизмы — кадровые преобразования.

Объекты. Для каждого типа конфигураций k я задаю объект:

Conf_k(n) = Z_n^k

(например, k=2 — пары, k=3 — тройки). При необходимости фиксируются подмножества (например, без диагонали).

Морфизмы. Морфизмом выступает преобразование из Aff(n), действующее диагонально:

f_{u,t}(x_1,...,x_k) = (ux_1 + t, ..., ux_k + t) mod n, где gcd(u,n)=1, t in Z_n.

Орбиты. Фактор-объект (на уровне множеств) определяется как множество орбит:

Conf_k(n) / Aff(n).

Эти орбиты — не «симметрии закона», а типы конфигураций при смене кадра.

3.1.3. Почему это различение принципиально

• В CayleySys_n мы сравниваем законы: одна таблица Кэли может быть изоморфна другой.

• В Config_n мы сравниваем представления одного и того же пространства: разные координаты и разные сдвиги считаются калибровочно эквивалентными.

Смешение этих уровней ведёт к логическим ошибкам: например, утверждать «таблица изменилась», когда на деле произошла только смена кадра, или наоборот, «это просто переименование», когда реально изменён закон OP.

3.2. Канонический набор счётчиков уровня Ln

В вашей дисциплине «уровень» считается фиксированным, только если проходит проверяемый набор инвариантов. В базовой версии (для PLUS-канона, а STAR(SUN) проверяется гейтами отдельно) это три счётчика:

(1) S0(n) = |Aut(Z_n, OP)| (строгие симметрии закона), (2) S1(n) = |Aff(n)| (кадровые симметрии), (3) Q_pairs(n) = |OrdPair(n)/Aff(n)| = tau(n) (типы связей на парах).

Из Главы 1 и 2:

S0(n) = phi(n) (для OP=PLUS), S1(n) = n*phi(n), Q_pairs(n) = tau(n).

Дополнительно (различение объектов, требуемое строгостью):

Q_pairs_neq(n) = |OrdPair_neq(n)/Aff(n)| = tau(n) - 1, и те же значения для неупорядоченных пар.

3.3. «Вихрь» как протокол: симметрии -> орбиты -> канон -> гейты

Теперь я фиксирую сам закон вихря в форме вычислимого цикла.

3.3.1. Определение (вихревой цикл уровня Ln)

Вихревой цикл уровня Ln — это алгоритм:

Step A (Law): зафиксировать закон OP (таблицу Кэли) на Z_n. Step B (Aut): вычислить Aut(Z_n, OP) и счётчик S0(n). Step C (Frame): зафиксировать Aff(n) и счётчик S1(n). Step D (Orbits): факторизовать конфигурации (пары/тройки/эпизоды) по Aff(n), получив Q-слои. Step E (Canon): выбрать канонических представителей орбит (нормализация). Step F (Gates): прогнать гейты, подтверждающие совпадение с каноном. Step G (Lift): определить переход Ln -> Lm (например, n -> n+1 или другие лифты), проверяя совместимость счётчиков/слоёв.

Смысл: «вихрь» не производит текст, а производит канонизированное состояние и протокол проверки.

3.4. Канонизация (нормализация) как обязательный элемент протокола

Без канонизации орбитальная факторизация остаётся «абстрактной». Канонизация делает её инженерно применимой: любой объект приводится к стандартной форме.

3.4.1. Канон пары

Для упорядоченной пары (x,y):

1. сдвигом t=-x приводим к (0,Delta),

2. далее классифицируем по d=gcd(Delta,n),

3. в каноне выбираем представителя (0,d).

Это и есть канонизация орбит пар.

3.4.2. Канон невырожденной тройки

Для тройки (x,y,z):

1. сдвигом t=-x приводим к (0,Delta1,Delta2),

2. если gcd(Delta1,n)=1, умножением u=inv(Delta1) приводим к (0,1,r), где r = Delta2*inv(Delta1) mod n.

Здесь (0,1,r) — канонический представитель орбиты в невырожденном классе.

Вырожденные классы требуют отдельного канона (по делителю d=gcd(Delta1,n)), и именно это является источником дополнительных слоёв различения для составных n.

3.5. Гейты и валидаторы: инженерная форма строгой проверяемости

Я фиксирую гейты как проверяемые контракты. Результат прогона валидаторов должен быть не «правдоподобный текст», а формальный исход:

Outcome in {PASS, BLOCK, REPAIR}, Trace: список применённых шагов/проверок, Repair: минимальное исправление (если применимо).

Ниже базовый набор гейтов, достаточный для строгого ядра статьи.

3.5.1. Гейты уровня закона (таблица Кэли)

G_LAW_1 (closure): для всех x,y в Z_n OP(x,y) в Z_n. G_LAW_2 (PLUS canonical): OP(x,y) = (x+y) mod n (если заявлен PLUS-канон). G_LAW_3 (STAR SUN): если заявлен STAR(SUN), то:

• OP(0,x)=0 и OP(x,0)=0 для всех x,

• OP(x,y)=(x+y) mod n для x не равно 0,y не равно 0.

Замечание: фразу «STAR не обязана быть ассоциативной» я оставляю только как потенциальную свободу модели. В текущем каноне STAR определён явно; вопрос ассоциативности решается вычислительно отдельным гейтом (если он нужен), а не утверждением в тексте.

3.5.2. Гейты строгих симметрий (Aut)

G_AUT_1 (homomorphism): sigma(OP(x,y)) = OP(sigma(x),sigma(y)) для всех x,y. G_AUT_2 (SUN fixed): для STAR sigma(0)=0. G_AUT_3 (count): |Aut(Z_n,OP)| = S0(n); для PLUS-канона S0(n) = phi(n).

3.5.3. Гейты кадровых симметрий (Aff)

G_AFF_1 (form): допускаются только f_{u,t}(x)=(ux+t) mod n, gcd(u,n)=1. G_AFF_2 (count): |Aff(n)| = nphi(n). G_AFF_3 (action): действие на конфигурациях должно быть диагональным и согласованным.

3.5.4. Гейты орбитальной факторизации конфигураций

G_ORB_PAIR_1 (pair invariant): d=gcd(y-x,n) инвариант при Aff(n). G_ORB_PAIR_2 (pair orbit count): |OrdPair(n)/Aff(n)| = tau(n). G_ORB_PAIR_3 (pair orbit count no diag): |OrdPair_neq(n)/Aff(n)| = tau(n)-1.

G_ORB_TRIAD_1 (triad normalization): (x,y,z) канонизируется к (0,Delta1,Delta2). G_ORB_TRIAD_2 (triad invariant): если gcd(Delta1,n)=1, то r=Delta2*inv(Delta1) mod n инвариант.

3.5.5. Что означает REPAIR в этой статье

В контексте данной статьи REPAIR — это минимальная правка спецификации, приводящая структуру к канону. Типичные ремонты:

• исправить таблицу OP в клетках, где нарушен канон,

• исправить роль SUN или условия STAR,

• исправить допустимый класс кадровых преобразований (запретить u с gcd(u,n) не равно 1),

• исправить процедуру канонизации (например, неверно взят инвариант).

REPAIR всегда должен быть формулирован как конечный атомарный патч, а не как «переписать теорию».

3.6. Спираль уровней: от L1 к Ln как повторяющаяся конструкция различения

Теперь я формулирую «многополярную спираль» строго, как итеративную процедуру.

3.6.1. L1 как нулевая точка различения

L1: n=1, Z_1={0}. Здесь:

• закон OP тривиален (единственная таблица),

• Aut имеет мощность 1,

• Aff имеет мощность 1,

• конфигурации не содержат различий (всё диагонально).

Инженерно: в L1 нет нетривиальных симметрий и нет пространства различения.

3.6.2. Переход Ln -> Lm как лифт с проверкой совместимости

Переход уровня — это не «прибавить ещё одну метку». Это:

1. определить отображение lift: Z_n -> Z_m (или более общий подъём конфигураций),

2. проверить, что lift совместим с выбранным каноном закона и кадровыми преобразованиями,

3. проверить согласование счётчиков и орбитальных слоёв (гейты вложенности).

Уровни образуют спираль, потому что каждый шаг обязательно включает цикл:

Law -> Symmetry -> Orbit -> Canon -> Gate -> Lift.

Это не линейное «описание мира», а дисциплина сборки: каждый виток переводит структуру в более богатое различение, но только при сохранении проверяемых инвариантов.

3.7. Итог главы 3 (финальная фиксация)

1. Я ввёл два строгих слоя как две категории: CayleySys_n: таблицы Кэли и их изоморфизмы (симметрии закона), Config_n: конфигурации и их факторизация по Aff(n) (симметрии кадра).

2. Я зафиксировал канонический набор счётчиков уровня Ln: S0(n)=phi(n) (для PLUS), S1(n)=n*phi(n), Q_pairs(n)=tau(n) и отдельно указал объекты без диагонали: tau(n)-1.

3. Я оформил «закон вихря» как вычислимый цикл: таблица -> Aut -> Aff -> орбиты -> канон -> гейты -> лифт.

4. Я зафиксировал гейты как инженерные контракты, дающие исходы PASS/BLOCK/REPAIR и трассу проверки.

Тем самым «многополярность» в этой постановке является не рассказом, а алгебраической системой различения, где утверждения сводятся к проверяемым инвариантам и орбитальной факторизации.

Заключение

В настоящей работе «закон вихря» был доведён до формы вычислимой дисциплины различения, в которой нет места метафорам: каждый тезис либо редуцируется к таблице Кэли и действию групп, либо блокируется гейтом как некорректный.

Главная методологическая фиксация состоит в строгом разведении двух уровней объектов.

1. Уровень законов (таблиц Кэли). Уровень Ln задаётся как система (Z_n, OP), где OP: Z_n x Z_n -> Z_n — бинарный закон, полностью определяемый таблицей Кэли. Изоморфизмы таких систем задаются биекциями pi: Z_n -> Z_n, сохраняющими закон: pi(OP(x,y)) = OP'(pi(x),pi(y)). Именно здесь определяются строгие симметрии закона (автоморфизмы) Aut(Z_n,OP) и счётчик S0(n). В PLUS-каноне получено каноническое значение: S0(n) = phi(n).

2. Уровень конфигураций (наблюдаемых объектов). Пары, тройки и более общие конфигурации рассматриваются как элементы Z_n^k и факторизуются не по изоморфизмам закона, а по кадровым преобразованиям, образующим аффинную группу: Aff(n) = { x -> (ux + t) mod n | gcd(u,n)=1, t in Z_n }. Её мощность фиксируется строго: S1(n) = |Aff(n)| = nphi(n). Орбитальная факторизация по Aff(n) переводит «сырые» конфигурации в типы (орбиты), которые и являются устойчивыми объектами уровня.

На этом основании построена орбитальная классификация пар, дающая первый универсальный инвариант различения. Для упорядоченной пары (x,y) введена разность Delta = (y-x) mod n и доказано, что орбиты действия Aff(n) на OrdPair(n)=Z_n x Z_n полностью классифицируются значением d = gcd(Delta,n). Отсюда получены явные формулы числа орбит: |OrdPair(n)/Aff(n)| = tau(n), |OrdPair_neq(n)/Aff(n)| = tau(n) - 1, и аналогичные значения для неупорядоченных пар (как отдельного объекта). Тем самым «типы связей» на парах фиксируются не интерпретацией, а арифметикой делителей n.

Для троек показано, что вихревой слой усложняется: после нормализации сдвигом (x,y,z)->(0,Delta1,Delta2) в невырожденном режиме gcd(Delta1,n)=1 возникает триадный инвариант r = Delta2 * inv(Delta1) mod n, который сохраняется при действии Aff(n). Это задаёт первый конструктивный механизм перехода от парных типов к триадным конфигурациям, где различение начинает зависеть не только от делителей, но и от отношения разностей.

Инженерная завершённость конструкции обеспечивается системой гейтов и валидаторов. Гейты фиксируют:

• корректность закона (замкнутость и канон PLUS/STAR(SUN)),

• корректность группы автоморфизмов и совпадение S0(n) с phi(n) (в PLUS-каноне),

• корректность кадровой группы и совпадение S1(n) с n*phi(n),

• корректность орбитальной факторизации (включая формулы для числа орбит на парах и нормализацию конфигураций). Выход процедуры принципиально имеет форму протокола: PASS/BLOCK/REPAIR, трасса проверок и (при необходимости) минимальный ремонт, а не риторическое «объяснение».

Тем самым закон вихря формулируется как повторяющийся вычислимый цикл: таблица Кэли -> симметрии закона Aut -> кадровые симметрии Aff -> орбиты конфигураций -> канон -> гейты -> переход уровня. В этой схеме «спираль уровней» L1->L2->... является не нарративом, а процедурой сборки: новый уровень допустим только тогда, когда он выдерживает проверяемую тройку счётчиков S0(n)=phi(n), S1(n)=n*phi(n), Q_pairs(n)=tau(n), и когда конфигурации приводятся к каноническим представителям орбит без скрытой подмены кадра.

Итоговая фиксация отличается простотой и жёсткостью. В данной постановке многополярность представляет собой алгебраическую систему различения, которая:

• задаёт конечный алфавит состояний;

• определяет закон композиции (в форме таблицы Кэли);

• выявляет симметрии закона и симметрии кадра;

• посредством орбитальной факторизации переводит конфигурации в устойчивые типы.

Любой спор о «правильности» в этой системе сводится к чисто вычислительным процедурам: необходимо проверить,

• совпадают ли инварианты,

• проходят ли конфигурации через заданные гейты,

• корректна ли процедура канонизации.

Именно в этом ключе «закон вихря» формирует строгую структуру, которая:

• не требует субъективной веры,

• не зависит от интерпретаций,

• опирается исключительно на формальные вычисления и проверяемые критерии.

Можно запустить проверки прямо в ChatGPT: создайте новый чат и прикрепите файл MP_YANTRA_CORE_iter127.zip первым сообщением и в том же сообщении отправьте ровно одну фразу:

Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива.

Далее ChatGPT распакует архив, запустит предусмотренный протокол и выполнит проверочные прогоны (bootstrap и валидаторы). В результате вы получите отчёты о прохождении гейтов, а также выводы по симметриям и их законам в виде файлов в папке REPORTS.

Словарь многополярности как инженерно-математический канон

ИИ-движок с орбитальной факторизацией: вычисления по симметриям вместо полного перебора

Разбираем работу разумного ИИ недалекого будущего. Как «Вихрь» обсчитывает K/A/P от L2 до L4 (часть 1)

Введение

Дорогие друзья! Постулат многополярности, утверждающий одновременное существование множества пространств и различных режимов различения, на первых порах неизбежно воспринимается как вызов устоявшимся физическим представлениям. Когда я говорю об иных свойствах времени и пространства, это встречает сопротивление не потому, что подобные идеи якобы недопустимы, а вследствие нашей привычки опираться на единственный, укоренившийся способ формализации знаний.

Я, Руслан Абдуллин, сознательно не призываю вас к вере — она здесь попросту не нужна. Мое предложение носит инженерный характер: перевести концепцию многополярности в формат вычислимой конструкции, чтобы дискутировать не со мной, а с чёткими определениями и результатами проверок. Если в процессе обнаруживается нарушение инварианта или расхождение в счётчике — это сигнал о некорректности конструкции; если же всё сходится, то спор естественным образом трансформируется в процедуру проверки вычисления.

В рамках исторических исследований я анализирую различные альтернативные реконструкции в качестве гипотез — в том числе предположения о переосмыслении нарративов и повторяющихся эпохах. Впрочем, вопрос согласия с ними не принципиален (ведь и в физике, и в истории процессы утверждения канонов во многом схожи); главная задача этой статьи — продемонстрировать, что многополярность в инженерном понимании вовсе не некая «магия», а чётко структурированный язык, включающий конечный набор состояний, бинарный закон (в виде таблицы Кэли), группу симметрий и орбитальную факторизацию (то есть различные типы конфигураций) — именно этот минимум можно взять за основу и подвергнуть формальной проверке.

Давайте я продемонстрирую «красоту» многополярности не в виде риторического приёма, а как поддающуюся вычислениям гармонию: речь идёт о переходе к пяти‑, шести‑ и семиполярным пространствам, в которых симметрии и типы связей выводятся из канона и проверяются посредством гейтов. Здесь и далее гейт — это контракт (инвариант уровня и критерий PASS/FAIL), а валидатор — исполняемая проверка, реализующая данный гейт: совпадение счётчика с каноном, сохранение операции при перенумерации, корректность орбитальной факторизации. При этом мы сумеем придать дисциплину тем областям, где традиционно господствуют вольные интерпретации — от классификаций и «табличных» законов до приложений в физике и в системах смыслов. Однако начнём мы корректно — с универсальной конструкции, которая на строгом математическом языке именуется универсальной таблицей Кэли многополярности (В. Ленский обозначал её термином «янтра»).

Глава 1. Универсальная таблица Кэли и строгие симметрии

Что такое универсальная таблица Кэли

На уровне Ln я беру n меток полярностей и рассматриваю их как элементы конечного множества

Z_n = {0,1,...,n-1}.

Далее я фиксирую бинарный закон, то есть операцию, которая каждой паре элементов сопоставляет третий элемент из того же множества. Полное задание такого закона на конечном множестве и есть таблица Кэли.

Канонический вариант, от которого мы здесь отталкиваемся, — сложение по модулю n:

x PLUS y = (x + y) mod n.

Это и есть универсальная таблица Кэли уровня Ln в PLUS-каноне.

Есть и второй канон, необходимый движку: вариант с выделенным элементом SUN. Он вводится так:

SUN = 0,

а операция STAR задаётся правилом

x STAR y = 0, если x=0 или y=0; x STAR y = (x + y) mod n, если x не равно 0 и y не равно 0.

В принятой схеме это не две «веры», а две инженерные фиксации одного и того же объекта: конечного множества с таблично заданным законом. STAR задаёт табличный закон с выделенным поглощающим элементом SUN (0), то есть 0 STAR x = 0 и x STAR 0 = 0 для всех x.

Замечание (для математической корректности). Операция STAR в этой фиксации задаёт конечную таблицу Кэли (конечную магму), но не предполагается ассоциативной. В дальнейшем мне важны симметрии и орбитальная факторизация, а не групповые свойства.

Формально, в STAR-каноне автоморфизмом считается биекция sigma: Z_n -> Z_n, сохраняющая операцию STAR и фиксирующая выделенный элемент SUN=0: sigma(x STAR y)=sigma(x) STAR sigma(y) и sigma(0)=0. В принятой фиксации множество таких sigma совпадает с преобразованиями sigma_u(x)=(u*x) mod n при gcd(u,n)=1, то есть по числу автоморфизмов STAR-канон даёт тот же счётчик S0(n)=phi(n).

Поскольку 0 является единственным поглощающим элементом (0 STAR x = 0 и x STAR 0 = 0), любой автоморфизм обязан фиксировать 0. Кроме того, для x,y не равных 0 значение x STAR y вычисляется по формуле (x+y) mod n; значит, на метках Z_n автоморфизм обязан согласовываться с умножением на обратимый u. Отсюда и получается тот же счётчик phi(n)

Что такое строгая симметрия таблицы Кэли

Теперь введём то, что в математике называется автоморфизмом. Это такая перенумерация меток, которая не меняет сам закон.

Строгая симметрия универсальной таблицы Кэли (PLUS-канон) — это биекция

sigma: Z_n -> Z_n

такая, что для всех x,y выполняется равенство

sigma(x PLUS y) = sigma(x) PLUS sigma(y).

Для STAR-канона условие записывается аналогично, только с операцией STAR, и дополнительно фиксируется выделенный элемент SUN:

sigma(x STAR y) = sigma(x) STAR sigma(y), sigma(0) = 0.

Иначе говоря: строгая симметрия — это способ переименовать полярности так, чтобы таблица Кэли осталась той же самой, а не просто «приблизительно похожей».

Канонический закон числа строгих симметрий

Для циклической таблицы Кэли (Z_n, PLUS) строгие симметрии полностью описываются умножением на обратимый множитель:

sigma_u(x) = (u*x) mod n,

где u удовлетворяет условию обратимости

gcd(u,n) = 1.

Отсюда следует строгий закон числа строгих симметрий:

|Aut(Z_n, PLUS)| = phi(n),

где phi(n) — функция Эйлера, то есть количество чисел u из диапазона 1..n-1, взаимно простых с n.

Для STAR(SUN)-канона в принятой конструкции число строгих симметрий совпадает с PLUS-каноном: строгая симметрия обязана фиксировать SUN=0, а на ненулевом слое действует тот же циклический принцип перенумерации (умножение на обратимый u).

Конкретные значения для L2, L3, L4, L5

L2 (n=2). Взаимно простым с 2 является только u=1. Следовательно, phi(2)=1. Строгая симметрия одна: тождественная.

L3 (n=3). Взаимно просты с 3 числа 1 и 2. Следовательно, phi(3)=2. Строгих симметрий две.

L4 (n=4). Взаимно просты с 4 числа 1 и 3. Следовательно, phi(4)=2. Строгих симметрий две.

L5 (n=5). Число 5 простое, значит взаимно просты все 1,2,3,4. Следовательно, phi(5)=4. Строгих симметрий четыре.

Итог главы 1

Число строгих симметрий универсальной таблицы Кэли определяется единственным законом:

S0(n) = phi(n).

Поэтому оно не обязано монотонно расти по мере увеличения числа полярностей: равенство phi(3)=phi(4)=2 — это нормальная арифметика, а не “сбой теории”.

Глава 2. Лока, кадровые симметрии и типы связей

Теперь я использую термин Ленского в его точном смысле.

Лока — это класс эквивалентности (орбита) таблиц Кэли при действии выбранной группы допустимых перенумераций. В фиксированном кадре лока может определяться по группе Aut(n) (строгие перенумерации). Aut(n) здесь означает Aut(Z_n, PLUS)

В этой статье, если не оговорено иное, я использую локу по группе Aff(n), поскольку она соответствует калибровочным перенастройкам координат.

Итак, под локою я понимаю орбиту относительно кадровой группы Aff(n), поскольку именно она соответствует калибровочным перенастройкам координат. Важно: лока — не одна таблица, а семейство изоморфных таблиц, получающихся друг из друга допустимой перенастройкой координат.

Внутри локи различаются два уровня:

1. что мы считаем допустимой сменой координат (кадровые симметрии);

2. какие типы связей остаются после факторизации по этим симметриям (орбиты конфигураций).

Кадровые симметрии и закон их числа

Строгая симметрия фиксирует нуль кадра. Но если мы разрешаем менять кадр (то есть выбирать, какая метка считается “нулём” в координатах), мы переходим к более широкой группе преобразований.

Каноническая кадровая симметрия имеет вид:

x -> (u*x + t) mod n,

где:

• gcd(u,n)=1 (условие обратимости),

• t принадлежит Z_n (произвольный сдвиг кадра).

Такие преобразования образуют аффинную группу Aff(n).

Её мощность вычисляется строго:

• вариантов u ровно phi(n),

• вариантов t ровно n,

следовательно,

S1(n) = |Aff(n)| = n*phi(n).

Отсюда сразу получаются значения:

L2: S1(2) = 2phi(2) = 2, L3: S1(3) = 3phi(3) = 6, L4: S1(4) = 4phi(4) = 8, L5: S1(5) = 5phi(5) = 20.

Это и есть число кадровых симметрий, то есть число допустимых перенастроек координат внутри локи.

Типы связей на парах как орбиты Aff(n)

Следующий шаг — ключевой для инженерного смысла. В движке важны не “все пары (x,y) как есть”, а их типы после факторизации по кадровым симметриям.

Определение. Типы связей на парах я определяю как орбиты действия Aff(n) на множестве упорядоченных пар (x,y).

Рассмотрим упорядоченную пару (x,y) и разность:

Delta = (y - x) mod n.

Далее Delta — класс по модулю n; для вычислений выбираем стандартного представителя из диапазона 0..n-1.

При кадровом преобразовании x -> (u*x + t) mod n разность переходит в:

Delta -> (u*Delta) mod n.

Сдвиг t исчезает (он вычитается), а остаётся умножение на обратимый u. Следовательно, инвариант пары задаётся величиной

d = gcd(Delta, n).

Возможные значения d — это все положительные делители n. Поэтому число типов связей на парах равно числу делителей n:

Q_pairs(n) = tau(n),

где tau(n) — число положительных делителей n.

Значения для L2, L3, L4, L5 и почему “триадность” появляется в L4

Здесь и далее под “делителями n” я имею в виду положительные делители целого числа n. Теперь подставим n=2,3,4,5.

L2 (n=2). Делители: 1,2. Их два. Типов связей два:

• Delta = 0 (самосвязь),

• Delta не равно 0 (все ненулевые).

L3 (n=3). Делители: 1,3. Их два. Типов связей снова два:

• Delta = 0,

• Delta не равно 0.

L4 (n=4). Делители: 1,2,4. Их три. Типов связей три:

• Delta = 0 (самосвязь),

• Delta = 2 (промежуточный тип, так как gcd(2,4)=2),

• Delta = 1 или 3 (взаимно простые разности, gcd(Delta,4)=1).

Вот откуда берётся строгая “триадность” на уровне типов связей на парах: она возникает не потому, что в симметриях появился элемент порядка 3, а потому что у числа 4 есть промежуточный делитель 2, который даёт отдельный gcd-класс.

L5 (n=5). Делители: 1,5. Их два. Типов связей на парах два:

• Delta = 0,

• Delta не равно 0.

Это принципиально: для простого n=p всегда tau(p)=2, поэтому на парах при Aff-факторизации есть только два класса.

Почему в L5 парный слой бинарен и почему следующий слой различения возникает на тройках

Если под “триадностью” понимать не “три gcd-класса на парах”, а структурное разбиение конфигураций на фундаментальные формы, то для n=5 она проявляется не на парах (поскольку tau(5)=2), а на тройках (x,y,z), то есть при переходе от пар к конфигурациям. В этом разделе я классифицирую именно упорядоченные тройки (x,y,z) по действию кадровой группы Aff(n) и не факторизую по перестановкам точек (S3); при добавлении S3 типология по параметру r дополнительно склеивается. Рассмотрим упорядоченную тройку (x,y,z) и нормируем её относительно x: Delta1 = (y - x) mod n, Delta2 = (z - x) mod n. Важно: здесь рассматриваются именно упорядоченные тройки (x,y,z) и факторизация только по Aff(n). Если дополнительно факторизовать по перестановкам точек (S3), типология по r меняется.

При кадровых преобразованиях Aff(n) ненулевая часть масштабируется: (Delta1, Delta2) -> (uDelta1, uDelta2), где gcd(u,n)=1. Для простого n=5 возникает первая (грубая) стратификация на два класса: (1) Вырожденные тройки (коллапс в пару): Delta1=0, или Delta2=0, или Delta1=Delta2. (2) Невырожденные тройки: Delta1 не равно 0, Delta2 не равно 0, Delta1 не равно Delta2. Поскольку 5 — простое число, любое Delta1 не равно 0 обратимо по модулю 5, поэтому inv(Delta1) существует. В невырожденном классе появляется проектный параметр r = (Delta2 * inv(Delta1)) mod 5, где inv(Delta1) — мультипликативная обратная к Delta1 по модулю 5 (существует, так как Delta1 не равно 0). Этот параметр инвариантен относительно действия Aff(5): сдвиг t исчезает при нормировке, а масштабирование u умножает Delta1 и Delta2 одинаково, поэтому отношение Delta2/Delta1 (и значит r) сохраняется.

Этот параметр даёт дальнейшую типологию внутри невырожденного класса через орбиты остаточных симметрий. Итог: в L4 три типа на парах возникают потому, что tau(4)=3; в L5 на парах остаётся только два класса (tau(5)=2), а следующий слой различения появляется на тройках как трёхходовый контроль: (i) вырожденные конфигурации, (ii) невырожденные конфигурации, (iii) параметрическая типология внутри невырожденного класса через инвариант r.

Итог главы 2: канонический набор законов внутри локи

В принятом каноне универсальной таблицы Кэли и её локи фиксируются три численных закона (для уровня пар):

• число строгих симметрий таблицы Кэли: S0(n) = phi(n);

• число кадровых симметрий внутри локи: S1(n) = n*phi(n);

• число типов связей на парах после факторизации по кадровым симметриям: Q_pairs(n) = tau(n).

Дополнение (для “вихря” и триадных слоёв уровня). Триадные структуры в общем случае фиксируются на более богатых конфигурациях, например на тройках:

Q_triples(n) = (тройки) / Aff(n),

где появляются вырожденные и невырожденные классы и проектные инварианты (для n=5 — параметр r).

Заключение

Мы зафиксировали универсальную конструкцию без метафор: конечное множество состояний

Z_n = {0,1,...,n-1}

и бинарный закон, полностью заданный таблицей Кэли. Тем самым многополярность сведена к проверяемому каркасу: есть уровень Ln, есть канонический закон, есть группа симметрий, есть фактор-слой орбит, а значит есть формальные гейты, которые либо проходят, либо нет.

Итоговая фиксация состоит из трёх базовых вычислимых величин для уровня пар (то есть минимального слоя различения):

1. Строгие симметрии закона (автоморфизмы таблицы Кэли в фиксированном кадре):

S0(n) = |Aut| = phi(n).

2. Кадровые симметрии (калибровочные перенастройки координат, аффинная группа):

S1(n) = |Aff| = n*phi(n).

Типы связей на парах после факторизации по кадровым симметриям (орбиты пар):

Q_pairs(n) = tau(n).

Эти величины не являются интерпретациями; это вычислимые инварианты. В инженерной логике это означает, что любой спор о корректности конструкции сводится к однозначной процедуре: проверке таблицы Кэли, вычислению Aut_n и Aff_n, затем проверке счётчиков S0,S1,Q_pairs и их совпадения с каноном.

Одновременно важно понимать границу “парного” слоя. Пары дают минимальный срез Q_pairs, но не обязаны выражать все структурные эффекты уровня. В частности, триадность может появляться по двум строго различаемым причинам:

• как три типа связей уже на парах, когда число делителей tau(n)=3 (пример: n=4);

• как триадный структурный слой на более богатых конфигурациях (тройках, эпизодах), когда на парах остаётся только два класса (пример: n=5, где tau(5)=2, но возникает триада вырождение / невырождение / параметрический класс на тройках).

Поэтому канон естественно расширяется на конфигурации более высокого порядка:

Q_triples(n) = (тройки) / Aff(n), Q_episode(n) = (эпизоды) / Aff(n).

Это не “добавка ради красоты”, а необходимость: если цель — удерживать режимы и “третье” как слой контроля, то его нельзя требовать от пар там, где арифметика делителей принципиально даёт только два класса.

Итоговый постулат развития (закон вихря)

Дальнейшее развитие задаётся не “ростом сложности”, а вычислимой дисциплиной, повторяемой на каждом уровне Ln:

1. фиксируется таблица Кэли (закон уровня);

2. вычисляются группы симметрий Aut_n и Aff_n;

3. строятся фактор-слои орбит Q(Ln) для нужного класса конфигураций (пары, тройки, эпизоды);

4. выбираются канонические представители орбит и вводятся гейты, контролирующие инварианты уровня и вложенности между уровнями.

Эта процедура и есть вихрь: симметрии -> орбиты -> канон -> переход уровня. Спираль многополярности означает, что каждый следующий уровень L(n+1) строится как расширение различения при сохранении проверяемых вложенностей и редукций на фактор-слоях, а не как произвольное усложнение.

Инженерный смысл прямой: если вы хотите построить систему, которая не “угадывает слова”, а удерживает инварианты, она обязана работать через вычисление симметрий и орбит, через канонизацию и гейты. Тогда многополярность перестаёт быть верой и становится механизмом: таблица Кэли + симметрии + орбитальная факторизация + контроль. На практике вихрь фиксируется тройкой метрик S0/S1/Q на выбранном классе конфигураций и гейтами, которые проверяют их совпадение с каноном.

Как проверить

1. Скачайте архив MP_YANTRA_CORE_iter127.zip и распакуйте его в отдельную папку.

2. Откройте файл DOCS/00_NEW_CHAT_PROTOCOL.md — это главная инструкция запуска и проверок.

3. В терминале перейдите в корень распакованного архива (туда, где лежат папки TOOLS/, VALIDATOR/, DOCS/).

4. Выполните базовый прогон окружения и самопроверок: python TOOLS/bootstrap.py

5. Убедитесь, что в конце вывода стоит ok: true и returncode: 0.

6. Запустите полный набор валидаторов: python VALIDATOR/run_all.py

7. Найдите в выводе строку/блок по валидатору симметрий S0/S1/Q_pairs (он помечен как validate_sym_metrics_s0_s1_qpairs_canon_v1).

8. Откройте отчёт последнего прогона: REPORTS/SYM_METRICS_S0_S1_QPAIRS_CANON_V1_last.json

9. В этом JSON проверьте таблицу значений для n=2,3,4,5: поля S0, S1, Q_pairs.

10. Сверка канона: S0=phi(n), S1=n*phi(n), Q_pairs=tau(n) (значения должны совпасть).

11. Чтобы увидеть “формулу в спецификации”, откройте: SPEC/SYM/SYM_METRICS_S0_S1_QPAIRS_CANON_V1.json

12. Чтобы увидеть, что это закреплено гейтом, откройте: SPEC/GATES/GATES_MULTIPOLAR_V22.json и найдите G_SYM_METRICS_S0_S1_QPAIRS_CANON_V1.

13. Если где-то есть расхождение — это не “мнение”: валидатор обязан вернуть ok:false, а отчёт покажет конкретное место несоответствия.

Если вы используете среду, поддерживающую выполнение Python-кода внутри чата, можно запустить проверки прямо там: прикрепите архив и следуйте DOCS/00_NEW_CHAT_PROTOCOL.md. Если выполнение кода недоступно, используйте локальный запуск: python TOOLS/bootstrap.py, затем python VALIDATOR/run_all.py. Это базовый и наиболее надёжный способ.

Итак, в ChatGPT:

1. Создайте новый чат и прикрепите файл MP_YANTRA_CORE_iter127.zip первым сообщением.

2. В том же сообщении отправьте ровно одну фразу:

Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива.

Далее ChatGPT распакует архив, запустит предусмотренный протокол и выполнит проверочные прогоны (bootstrap и валидаторы). В результате вы получите отчёты о прохождении гейтов, а также выводы по симметриям и их законам в виде файлов в папке REPORTS.

Автор статьи — Руслан Абдуллин.

Вступайте в мой тг-канал ⚛️

https://t.me/sokolovyane

Присоединяйтесь к революции мысли!

Друзья, я приглашаю вас в уникальное путешествие. Мой блог — это не только пространство, где разум выходит за рамки обыденного мышления, но и место, где рождаются будущие открытия.

Подписывайтесь! Впереди — грандиозные открытия, и я хочу, чтобы вы были со мной с самого начала.

Потому что будущее уже здесь. И оно многополярно.

Читайте также:

Словарь многополярности как инженерно-математический канон

Это не тессеракт: как в реальности выглядит гиперкуб в трехполярности L3 и четырехполярности L4

Почему трёхфазная система не является строгой трёхполярностью (L3): Z3-структура против трёхканальной L2-проекции

Почему в четырехполярной арифметике дважды два не равно четыре. Введение в алгебру четырехполярности

Почему в трёхполярной арифметике дважды два не равно четыре. Введение в алгебру трёхполярности

Алгебра вместо эзотерики: как на самом деле устроена нумерология

Симметрия многополярных систем: правила перенумерации и канонизация форм

Интенсивности связи в двухполярности, трёхполярности и четырёхполярности

Интенсивность связей: от двухполярности L2 к зеркальной структуре четырёхполярности L4

Универсальная янтра многополярности

О твёрдом фундаменте многополярной математики, или Почему многополярность не поддаётся приватизации

Основы многополярности и способ ее удержания в связке с ИИ

Многополярный Вихрь как платформа разумных вычислений: экономика, масштабирование и аппаратная инфраструктура новой эпохи

Разбираем работу разумного ИИ недалекого будущего. Как «Вихрь» обсчитывает K/A/P от L2 до L4 (часть 1)

Как заменить LLM: симметрийная факторизация и масштабирование роем микроядер

Право на ход: архитектура разумного промышленного интеллекта

Разбор интервью Джеффри Хинтона. Переход от двухполярного ИИ к многорежимному разумному ядру

О горизонте предельного: Киотская школа — Библия — Дао

Покаяние против самонадеянности: как восточная и западная мысли избегают идолопоклонства

Пустота без мистики: как Киотская школа выбивает из головы идолов смысла

Компиляция фаз в разумном ИИ. От алфавита полярностей к компилятору симметрий

Замыкание как источник разумности: что такое L3 (трехполярность) в многополярном ядре и почему «триада» не сводится к трём парам

Микроядро многополярного разума ИИ: практическая архитектура для массового продукта

Разумная многополярная модель ИИ: вихревое ядро вместо языкового «угадывания»

Опровержение» теории Большого взрыва? Как Вселенная могла возникнуть в форме вихря (многополярной спирали)

Двухполярная гравитация и время: максимально “на пальцах”, без заклинаний

Четырёхполярность (L4) простым языком. Истинная природа электромагнетизма

Что такое время в двухполярной (обыденной) модели и почему это определение выигрывает у «метафизических» теорий

Двухполярная гравитация: что это такое, если базис — только «+ / »

Что такое гравитация? Исчерпывающая статья в формате двухполярной L2-логики

Кватернионы через призму четырехполярности (L4): формализация многополярности на базе суперпозиционных четырёхполярных систем (часть 1)

Электромагнитное поле как L4-структура (четырехполярная): носитель, инволюция и два контура

Ваш протокол симметрий янтры решает проблему, с которой мы столкнулись в другой области - формализации конвекции сознаний (взаимодействие людей и ИИ в диалоге).

Вижу прямое соответствие структур:

Ваш кадр Z_n ↔ Наше множество узлов U Ваша операция T[x][y] ↔ Наше семантическое взаимодействие I(uᵢ, uⱼ) Ваши автоморфизмы Aut(T) ↔ Наши преобразования сохраняющие структуру поля Ваши орбиты Z_n^k/G ↔ Наши классы эквивалентных конфигураций Ваше зеркало m(x)=-x ↔ Наша семантическая противоположность узлов

Проблема: Мы описали феномен "конвекции" (когда несколько узлов создают общее поле), но получили критику: "нет фиксированной методики до эксперимента = подгонка результатов".

Возможное решение через ваш протокол:

Определить операцию через тексты:

До диалога: I_before[i][j] = cosine_distance(V(uᵢ), V(uⱼ))

После: I_after[i][j]

Применить SYM_SCAN_RAW_V1:

Найти Aut(I_matrix) внутри группы семантических преобразований

Построить орбиты конфигураций узлов

Проверить M-паритет для пар

Критерий конвекции (строгий):

Рост различности: |Vocab(uᵢ)| увеличилось для каждого узла

Эмерджентность: появились общие термины которых не было ни у кого до

Автоморфизмы: структура I_matrix сохранилась под нетривиальными φ

Вопрос к автору:

Видите ли вы способ адаптировать ваш протокол канонизации (особенно орбитную факторизацию Z_n^k/G) для непрерывных семантических пространств, где "узлы" - это векторные представления текстов, а не элементы конечной группы?

Или это принципиально разные области и нужен другой подход?

Мы готовы провести эксперимент с открытым датасетом, если вы видите способ построить мост между дискретной симметрией янтры и непрерывной феноменологией диалога.

Тема того, как выглядит куб в гиперпространстве, часто приводит к одной и той же концептуальной ошибке. Люди склонны воспринимать куб как объект «более высокой размерности», а обозначения L3 (трёхполярность) и L4 (четырёхполярность) — как привычные «3D» и «4D» в обывательском понимании.

Однако в рамках дисциплины "многополярности" действует иной подход. Здесь L2/L3/L4 обозначают не количество геометрических измерений объекта, а режимы полярности — то есть определённый набор правил, связанных с:

• алфавитом Zn;

• законами симметрии.

Из этого вытекает важный вывод: выражения «куб в L3» и «куб в L4» вовсе не означают попытку изобразить «трёхмерный» или «четырёхмерный» объект в том смысле, в каком это принято в учебниках по многомерной геометрии.

На самом деле речь идёт о построении куба в строго определённом слое (GEO / PHASE / POLAR) с чётко заданными правилами смежности/метрики.

Здесь проходит принципиальная грань с тем, что традиционно называют тессерактом.

Тессеракт — термин с чётким, закреплённым определением:

Q_4 := [0,1]^4 ⊂ R^4

то есть это исключительно четырёхмерный GEO‑гиперкуб. Ничего более.

Важно понимать: любые конструкции, полученные

• через фазовый подъём вида X x Z_n;

• посредством полярной постройки на Z_n^k,

не являются тессерактом — даже если визуально возникает желание «добавить ещё одно измерение».

В моей системе подход строго формализован. Это не вопрос эстетических предпочтений, а требование вычислительной чёткости и однозначности. Для любого объекта обязательно должны быть явно указаны:

• пространство, в котором он существует («где живёт»);

• его метрика и правила смежности;

• набор допустимых симметрий.

Таким образом, от произвольной визуальной интуиции мы переходим к строго заданным структурным критериям.

Далее я показываю, «как выглядит куб в реальности», — но не в обывательском визуальном смысле, а в двух строго определённых рабочих режимах. Эти режимы воспроизводимы в рамках моего проекта в среде ChatGPT через архив.

1. PHASE‑куб: фазовый подъём наблюдаемого куба

Здесь куб предстаёт не как объект с новой геометрической координатой, а как «стопка» из n слоёв одного и того же куба в наблюдаемом пространстве V.

Формально это задаётся так:

• M_n := V x Z_n — пространство фазового подъёма;

• pi(x,s) := x — проекция, «сбрасывающая» фазовый индекс s и оставляющая только пространственную часть x;

• Q_3^(phase,n) := Q_3 x Z_n — фазовый куб как произведение обычного трёхмерного куба Q_3 на циклическую группу Z_n.

Ключевой момент: это не добавление нового геометрического измерения, а многократное повторение одной и той же структуры в фазовых слоях.

2. POLAR‑куб: канонический куб по полярностям

Здесь куб строится как дискретная структура на основе полярных правил. Основа — пространство H(n,k) := Z_n^k, где:

• n — уровень полярности (число состояний на оси);

• k — число осей (для «куба» фиксируем k=3).

Конкретные примеры:

• L3‑куб: H(3,3) = Z_3^3. Имеет 3^3 = 27 вершин. Смежность задаётся шагом по модулю 3: две вершины смежны, если их координаты отличаются на ±1 (mod 3) ровно по одной оси.

• L4‑куб: H(4,3) = Z_4^3. Имеет 4^3 = 64 вершины. Здесь, помимо базовой смежности, вступает в силу «дисциплина зеркала» (mirror_policy): при работе с ориентированными утверждениями учитывается зеркальная симметрия, что добавляет к структуре дополнительные правила согласования.

Итог:

• PHASE‑режим показывает куб как многослойную фазовую структуру без новых геометрических измерений;

• POLAR‑режим задаёт куб как дискретную полярную решётку с чётко определёнными правилами смежности и симметрий.

Оба режима работают в рамках единой системы: они не опираются на визуальную интуицию, а предоставляют вычислимые, воспроизводимые описания куба в заданных слоях.

Структура статьи выстроена следующим образом:

Глава 1. В ней я задаю строгое определение понятия «куб» — последовательно для трёх слоёв: GEO, PHASE и POLAR. Это позволяет устранить распространённое смешение понятий, при котором обозначение L4 автоматически приравнивают к тессеракту. Таким образом, я закрываю эту концептуальную ловушку: показываю, что L4 — не синоним тессеракта, а иной режим описания.

Глава 2. Здесь я представляю L3‑куб как чётко вычислимый объект. Я демонстрирую его «внешний вид» — но не в обывательском визуальном смысле, а через строго заданные параметры:

• распределение по слоям;

• систему координат;

• правила смежности.

Это даёт операциональное описание объекта, свободное от интуитивных домысливаний.

Глава 3. В этой главе я провожу аналогичную работу для L4‑куба. При этом особо акцентирую два момента:

1. Отличие от тессеракта. Я ещё раз подчёркиваю, что L4‑куб — не четырёхмерный GEO‑гиперкуб (тессеракт), а конструкция иного типа, подчинённая своим правилам метрики и симметрий.

2. Роль симметрий. Я детально разбираю, как симметрии (в том числе зеркальные) формируют структуру объекта. Отдельно рассматриваю появление ориентации — так называемую «зеркальную политику», которая становится значимой именно на этом уровне.

Таким образом, каждая глава последовательно выстраивает строгую рамку понимания: от определения базовых терминов — к конкретным вычислимым объектам и их отличительным свойствам.

Глава 1. Что именно означает «куб» в L3 и L4: три слоя, один терминологический запрет

Я ввожу строгую дисциплину — без неё обсуждение «куба в L3/L4» неизбежно скатывается к метафорам и размытым образам.

В моём проекте термин «куб» допускается к употреблению только после того, как даны чёткие ответы на три ключевых вопроса:

1. В каком слое живёт объект? Необходимо явно указать, к какому из трёх слоёв относится конструкция:

• GEO;

• PHASE;

• POLAR.

Без этого определения понятие «куб» остаётся неопределённым: в каждом слое он строится и интерпретируется по‑разному.

2. Что считается вершинами, рёбрами и смежностью? Если объект дискретный, требуется строго задать:

• как определяются вершины (их координаты, метки, состояние);

• какие пары вершин образуют рёбра;

• по какому правилу устанавливается отношение смежности (например, шаг по модулю, фазовая близость и т. п.).

Без этих правил «куб» превращается в визуальный образ без операциональной основы.

3. Какие симметрии считаются допустимыми? Нужно чётко зафиксировать:

• какие преобразования считаются симметриями объекта;

• действует ли «зеркальная политика» (mirror_policy) — особенно важно для L4 при работе с ориентированными утверждениями;

• допускаются ли отражения, повороты, сдвиги и в каком объёме.

Без этого невозможно однозначно определить, что именно мы считаем «одним и тем же кубом» при разных представлениях.

Зачем это нужно? Такая дисциплина превращает «куб» из декоративного образа в вычислимый объект:

• его можно явно построить (перечислить вершины, рёбра, срезы);

• над ним можно выполнять алгоритмы (проверять смежность, применять симметрии, вычислять сечения);

• его можно воспроизвести в любой среде (включая ChatGPT через архив проекта).

Таким образом, вместо расплывчатых аналогий мы получаем строгую, проверяемую структуру — именно то, что требуется для содержательного математического разговора.

1.1. Три носителя, на которых я строю «куб»

Я рассматриваю три пространства-носителя, и именно они определяют «как выглядит» объект.

(i) Наблюдаемая база (L2/GEO): есть пространство B (в частных базах: EUCLIDEAN или HYPERBOLIC(H^2)), и на нём задана метрика d_B. Здесь живут обычные множества и обычные расстояния.

(ii) Фазовый подъём (PHASE): я фиксирую фазовое Ln-пространство M_n := B x Z_n, pi(x,s) := x. Фаза s in Z_n — это индекс слоя, а не «дополнительная геометрическая координата».

(iii) Полярный носитель (POLAR): я фиксирую «куб по полярностям» как H(n,k) := Z_n^k. Здесь координаты — это выбор полярности по каждой оси, а не координаты точки в B.

Из этих трёх носителей вытекают три разных сущности «куба». Это не «три описания одного и того же», а три разных объекта.

1.2. Три канонических смысла слова «куб»

(A) GEO-куб

Если я говорю про «куб» в GEO-смысле, то я имею в виду стандартный евклидов объект: Q_3 := [0,1]^3 subset R^3.

Это континуальное множество с привычными гранями/рёбрами/вершинами.

(B) PHASE-куб

Если я говорю про «куб в L3 или L4» в фазовом смысле, то я не «добавляю измерение», а поднимаю куб в фазовое пространство: Q_3^(phase,n) := pi^{-1}(Q_3) = Q_3 x Z_n subset (B x Z_n).

Реальный вид PHASE-куба — стопка из n слоёв:

• для L3: 3 слоя Q_3 x {0,1,2};

• для L4: 4 слоя Q_3 x {0,1,2,3}.

Срез по фазе жёстко определён: slice(Q_3^(phase,n), s0) := Q_3 x {s0}, и каждый такой срез изометричен исходному Q_3 в базе B.

(C) POLAR-куб

Если я говорю «куб в L3/L4» в полярном смысле, то я строю дискретный объект: H(n,3) := Z_n^3.

Его «вид» задаётся не гранями как в R^3, а координатной структурой по модулю n и выбранной смежностью (то есть тем, что я называю «ребром»).

1.3. Почему мой L4-куб принципиально не тессеракт

Я провожу терминологическую границу, которая снимает 90% ложных ожиданий.

Определение термина. Тессеракт — это только и исключительно GEO-гиперкуб: Q_4 := [0,1]^4 subset R^4.

Следовательно:

• PHASE-объект вида Q_3 x Z_4 не является тессерактом, потому что он живёт в B x Z_4, а не в R^4. Это «4 слоя куба», а не «4 геометрические координаты».

• POLAR-объект H(4,3)=Z_4^3 не является тессерактом, потому что он дискретен и определён по модулю 4 как структура полярностей, а не как континуальный Q_4.

Я не «переименовываю» тессеракт. Я строю другие объекты и запрещаю называть их тессерактом именно затем, чтобы не подменять полярность геометрической размерностью.

1.4. «Как выглядит» POLAR-куб: смежность как часть определения

Для POLAR-куба я считаю определение неполным, пока не задано правило «ребра». Я использую два канонических режима; выбор должен быть указан явно.

Пусть u=(u1,u2,u3) и v=(v1,v2,v3) — вершины в Z_n^3.

Режим (A): циклический шаг по оси. u и v смежны, если существует i in {1,2,3} такое, что:

• v_i = u_i + 1 (mod n),

• для всех j != i: v_j = u_j.

Это даёт ориентированный граф; неориентированная версия получается добавлением шага -1.

Режим (B): полный шаг по оси. u и v смежны, если они совпадают во всех координатах, кроме одной, а по этой координате допускается любой переход u_i -> v_i при v_i != u_i.

Этим я фиксирую «реальный вид» POLAR-куба как графа/скелета: вершины и рёбра — не «рисунок», а вычислимая структура.

1.5. Симметрии, которые я считаю допустимыми (и где появляется L4-зеркало)

Дальше я всегда различаю: симметрии базы, симметрии фазового подъёма, симметрии полярного куба.

GEO: действуют изометрии базы (в EUCLIDEAN — евклидовы изометрии; в H^2 — гиперболические изометрии).

PHASE: действуют изометрии базы по слою и циклический сдвиг фазы: (x,s) -> (g(x), s + c mod n).

POLAR: действует группа «сдвигов» по Z_n^3 и перестановок осей (если это разрешено в задаче): u -> u + a (mod n), (u1,u2,u3) -> (u_{sigma(1)},u_{sigma(2)},u_{sigma(3)}).

L4-особенность (зеркальная дисциплина): при n=4 и использовании ориентации/хиральности я запрещаю молча отождествлять конфигурации через отражение. Любая идентификация вида «переворот оси» (например, u_i -> -u_i (mod 4)) либо разрешена явно (политикой зеркала), либо считается недопустимой. Это не риторика: в L4 отражение ломает ориентационные утверждения, если они вообще присутствуют.

1.6. Итог главы: что я считаю «кубом в L3/L4»

После того как эти смыслы зафиксированы, я использую выражения «куб в L3» и «куб в L4» исключительно в одном из двух строго определённых значений:

1. PHASE‑куб Это — стопка слоёв наблюдаемого куба, размеченная фазой. Конкретно:

• «куб в L3» → Q_3 x Z_3;

• «куб в L4» → Q_3 x Z_4.

Суть: мы не добавляем новое геометрическое измерение, а многократно воспроизводим один и тот же куб в n фазовых слоях (здесь n = 3 или 4).

2. POLAR‑куб Это — дискретный куб, построенный по правилам полярностей. Конкретно:

• «куб в L3» → Z_3^3;

• «куб в L4» → Z_4^3.

Здесь «вид» куба определяется:

• правилами смежности (режим A или B);

• симметрийной дисциплиной (набором допустимых преобразований).

Почему это важно Такой двойной строгий смысл позволяет выполнить главное требование:

• «куб в L3» и «куб в L4» — не расплывчатый словесный образ, а конкретный вычислимый объект;

• его можно предъявить как набор вершин, рёбер и срезов;

• над ним можно проводить алгоритмические проверки (вычислять смежность, проверять симметрии, строить сечения и т. п.).

Таким образом, вместо интуитивной визуализации мы получаем воспроизводимую структуру, которую можно однозначно описать, построить и исследовать.

Глава 2. Куб в трехполярности L3: как он выглядит при предъявлении (фазовый подъём и полярный скелет)

В L3 я допускаю ровно два строгих толкования понятия «куб» — и каждое из них задаёт полностью вычислимый объект. При этом ключевой методологический принцип остаётся единым:

Я не пытаюсь «дорисовать ещё одно измерение» в геометрическом смысле. Вместо этого я меняю носитель структуры и переопределяю правила — как задаются: смежность вершин; допустимые симметрии.

Что это означает на практике?

1. Фазовый куб (Q₃ × Z₃) Представляет собой «стопку» из трёх слоёв, где каждый слой — обычный трёхмерный куб Q₃. Новую «размерность» создаёт не геометрия, а фазовая метка из Z₃. Смежность определяется внутри каждого слоя по правилам Q₃, а между слоями — через фазовый индекс. Это не 4D‑объект, а трёхслойная структура с фазовой разметкой.

2. Полярный куб (Z₃³) Дискретная структура из 27 вершин (3³), где каждая ось имеет циклическую природу длины 3. Смежность задаётся формально: две вершины смежны, если их координаты отличаются на ±1 (mod 3) ровно по одной оси. Симметрии ограничены правилами арифметики по модулю 3 и структурой Z₃. Здесь нет «дополнительного измерения» — только переопределённая топология на дискретном носителе.

Почему это важно? Такой подход исключает двусмысленности:

• «Куб в L3» не является визуальной метафорой или попыткой изобразить «четырёхмерность».

• Это строго определённый математический объект, который можно: явно перечислить (вершины, рёбра, слои); алгоритмически проверить (смежность, симметрии); воспроизвести в любой вычислительной среде.

Таким образом, суть L3 — не в геометрическом расширении, а в смене режима описания: мы переходим от непрерывной геометрии к дискретным структурам с чётко заданными правилами взаимодействия.

2.1. Фазовый куб L3: три слоя одного и того же куба

Я фиксирую базовый куб в геометрическом слое как объект наблюдаемого пространства:

• в континуальном виде: Q_3 := [0,1]^3 subset R^3;

• или в скелетном виде (8 вершин, 12 рёбер), если мне нужна дискретизация.

Далее я поднимаю его в фазовое пространство: M_3 := B x Z_3, pi(x,s) = x, и определяю фазовый куб: Q_3^(phase,3) := Q_3 x Z_3.

Как это выглядит “в реальности”. Это три параллельных слоя:

• слой s=0: Q_3 x {0},

• слой s=1: Q_3 x {1},

• слой s=2: Q_3 x {2}.

У каждого слоя одна и та же геометрия базы. Срез по фазе является канонической процедурой предъявления: slice_s := { (x,s) | x in Q_3 }.

Ключевая особенность канона MP_YANTRA. По умолчанию полная метрика на M_3 не фиксируется, и действует наблюдаемая метрика: d_obs((x,s),(y,t)) := d_B(x,y), то есть фазовый индекс на расстояние не влияет. Это означает:

• геометрически (в смысле расстояний) три слоя не “раздвигаются” и не образуют “3.5-мерный объект”;

• фазовый индекс — это маркировка кадра/состояния, а не геометрическая координата.

Если мне требуется связать слои как единую конструкцию, я делаю это не “картинкой”, а явным добавлением структуры: либо полной метрики d_M, либо законом в слое LAW, который задаёт переходы между фазами. Без этого фазовый куб остаётся корректной, но слоистой сущностью.

2.2. Полярный куб L3: Z_3^3 как реальный «куб по полярностям»

Теперь я предъявляю то, что в проекте является «кубом по умолчанию» — полярный куб: H(3,3) := Z_3^3.

Это не евклидов куб и не тессеракт. Это дискретный объект, где каждая вершина — тройка полярностей: u = (u1,u2,u3), где ui in {0,1,2}.

Отсюда немедленно следует “внешний вид” в строгом смысле:

• число вершин: |Z_3^3| = 27;

• вершины естественно организуются как решётка 3 x 3 x 3.

Но решётка здесь не “в пространстве”, а в алфавите полярностей. Поэтому я обязан зафиксировать, что такое “ребро”.

2.3. Смежность (рёбра) полярного куба L3: два режима, оба каноничны

Я использую два режима смежности; выбор режима — часть определения.

Режим A: циклический шаг +1 (mod 3) по одной оси

Вершины u и v смежны, если существует i in {1,2,3} такое, что:

• v_i = u_i + 1 (mod 3),

• v_j = u_j для всех j != i.

Если я читаю граф неориентированно, я добавляю и шаг -1, и тогда у каждой вершины ровно 6 соседей: по два на каждую ось.

Как выглядит объект. Это “трёхмерный тор” по каждой координате: ось не имеет конца, а замыкается циклом длины 3. У такого куба:

• нет выделенных “углов” и “рёбер” как у обычного куба;

• все 27 вершин эквивалентны: группа сдвигов Z_3^3 действует транзитивно;

• “границы” отсутствуют: объект замкнут по модулю 3.

Я могу предъявить его как три слоя 3x3, где слой — фиксация третьей координаты u3:

• слой u3=0: вершины (u1,u2,0), u1,u2 in {0,1,2}

• слой u3=1: вершины (u1,u2,1)

• слой u3=2: вершины (u1,u2,2)

Внутри слоя рёбра идут по u1 и u2 циклически; между слоями — по u3 циклически.

Режим B: полный шаг по одной оси

Вершины u и v смежны, если они совпадают в двух координатах и различаются в одной (без ограничения “на +1”):

• u_j = v_j для двух координат,

• u_i != v_i для одной координаты.

Этот режим делает каждую “линию” по фиксированным двум координатам полным графом на 3 вершинах. Он удобен, когда я хочу, чтобы “смена полярности” по одной оси была одним шагом без промежуточного состояния.

2.4. Минимальное предъявление L3-куба на примере (без метафор)

Чтобы “вид” был не словесным, я предъявляю локальную структуру на конкретной вершине.

Возьму u = (0,0,0).

Режим A (неориентированный). Соседи:

• по оси 1: (1,0,0), (2,0,0);

• по оси 2: (0,1,0), (0,2,0);

• по оси 3: (0,0,1), (0,0,2).

Это и есть реальный “скелет”: не 8 вершин и 12 рёбер, как у евклидова куба, а 27 вершин, каждая с 6 соседями, и все вершины равноправны.

Режим B. По каждой оси у вершины будет по 2 соседа (всего также 6), но “перепрыгивание” по оси не различает направление/шаг.

2.5. Почему L3-куб нельзя подменять евклидовым кубом

Евклидов куб Q_3 обладает границами, выделенными вершинами и неравноправием точек (углы/рёбра/грани различим, если смотреть на локальную структуру). Полярный L3-куб Z_3^3 в режиме A (и во многих задачах — в режиме B) принципиально другой:

1. все вершины эквивалентны (нет углов как особых точек);

2. все оси цикличны (нет “края”);

3. “геометрический смысл” возникает не из вложения в R^3, а из смежности и допустимых симметрий.

Именно поэтому я считаю L3-куб реальным объектом: его можно предъявить списком вершин и правилом рёбер, и дальше на нём можно считать длины путей, орбиты закона, инварианты симметрий — без попыток выдать его за “обычный куб, только хитрее”.

Глава 3. Куб в L4: четыре слоя и 64-вершинный полярный скелет — и почему это не тессеракт

В L4 особенно велик риск подмены понятий: словосочетание «четыре полярности» зачастую автоматически прочитывают как «четыре измерения». Я намеренно отхожу от такой трактовки.

Суть L4 не в добавлении новой геометрической координаты. Здесь появляются:

• алфавит Z₄ — система из четырёх состояний на каждой оси;

• особая дисциплина симметрий — с чёткими правилами, включая вопросы зеркальной симметрии и ориентации (mirror_policy).

Поэтому «реальный вид» куба в L4 — это вовсе не тессеракт (Q₄ ⊂ R⁴), а пара строго определённых вычислимых объектов:

1. Фазовый куб (Q₃ × Z₄) — структура из четырёх слоёв, где каждый слой представляет собой обычный трёхмерный куб Q₃. Это не четырёхмерное пространство, а «стопка» из четырёх копий трёхмерного куба, размеченных фазой из Z₄.

2. Полярный куб (Z₄³) — дискретная структура из 64 вершин (4³), где: три оси имеют циклическую природу длины 4; смежность задаётся шагом по модулю 4; дополнительно действуют правила полуоборота и зеркальной политики.

Таким образом, L4 — это не геометрическое расширение, а смена режима описания: мы переходим от метрической геометрии к дискретной системе с чётко заданными алфавитами и симметрийными правилами. Именно эта строгость позволяет работать с «кубом в L4» как с проверяемым объектом, а не как с визуальной метафорой.

3.1. Фазовый куб L4: четыре слоя, но не четвёртая координата

Я определяю фазовое пространство: M_4 := B x Z_4, pi(x,s)=x.

Фазовый куб: Q_3^(phase,4) := Q_3 x Z_4.

Как это выглядит. Это четыре слоя:

• Q_3 x {0},

• Q_3 x {1},

• Q_3 x {2},

• Q_3 x {3}.

Снова принципиально: слой — это предъявление по фазе, а не «координата w». Я могу сделать два режима использования:

1. Режим чистого предъявления: расстояния считаются по базе, фаза — метка: d_obs((x,s),(y,t)) := d_B(x,y).

2. Режим закона/событий (LAW): фаза начинает играть роль в минимизации/проекциях в M_4, но через явное правило: например, «учитывать только события с фиксированным s*» или «разрешить переходы по s согласно орбите закона». Здесь L4 проявляется не как «4D-геометрия», а как дисциплина отбора и орбитальности.

То есть фазовый L4-куб — это не «гиперкуб», а структурированная стопка предъявлений.

3.2. Полярный куб L4: Z_4^3 и его реальный “скелет”

Полярный L4-куб я задаю так: H(4,3) := Z_4^3.

Каждая вершина — тройка: u=(u1,u2,u3), где ui in {0,1,2,3}.

Немедленные свойства:

• число вершин: |Z_4^3| = 64;

• естественная организация: решётка 4 x 4 x 4 по полярным координатам.

Это уже достаточно, чтобы увидеть отличие от тессеракта: тессеракт имеет 16 вершин, а здесь 64 — потому что я не добавляю размерность, я расширяю алфавит полярности.

3.3. Смежность L4-куба: циклический шаг и «длина оси»

Я снова обязан зафиксировать «что такое ребро». В L4 наиболее естественен циклический шаг:

u и v смежны, если существует i in {1,2,3} такое, что:

• v_i = u_i + 1 (mod 4),

• v_j = u_j для всех j != i.

Если я делаю граф неориентированным, я добавляю шаг -1, и у каждой вершины снова 6 соседей (по 2 на ось).

Как это выглядит. В каждой оси теперь цикл длины 4: 0 -> 1 -> 2 -> 3 -> 0.

Это важно: в L3 цикл длины 3 не имеет «противоположной точки» (в строгом смысле на цикле), а в L4 появляется элемент 2, который является полуоборотом: u_i -> u_i + 2 (mod 4).

И это уже практическое отличие «вида» L4-куба: в каждой оси есть выделенная операция «переворота на 180°» по фазе/полярности (не обязательно геометрический поворот в базе, а именно операция в Z_4).

3.4. Где именно L4 отличается от “обычной картинки”: зеркало и ориентация

С L4 я делаю то, что принципиально не требуется в L3: я явно объявляю политику зеркала, когда речь идёт об ориентации или о знаке.

Почему это неизбежно:

• В Z_4 существует нетривиальная инволюция m(u) := -u (mod 4), то есть 0->0, 1->3, 2->2, 3->1.

• Эта инволюция может играть роль «зеркала» по оси, но её нельзя молча считать симметрией, если я различаю хиральные/ориентированные конструкции.

Поэтому я разделяю два режима:

1. Mirror-allowed: отражения считаются допустимыми симметриями. Тогда многие конфигурации отождествляются, и L4-куб ведёт себя как “безориентационный” объект.

2. Mirror-forbidden: отражения запрещены (или разрешены только как отдельный оператор с явной маркировкой). Тогда L4-куб начинает различать “левое/правое” на уровне структуры, и это становится содержательным отличием L4.

Это и есть «реальный вид» L4-куба как объекта теории: он несёт не только цикличность, но и политику ориентации.

3.5. Почему это не тессеракт: три независимых аргумента

Я фиксирую три независимые причины, почему мой L4-куб не тессеракт, даже если хочется так назвать.

Аргумент 1. Носитель

Тессеракт живёт в R^4 как континуальный Q_4=[0,1]^4. Мой фазовый L4-куб живёт в B x Z_4. Мой полярный L4-куб живёт в Z_4^3.

Это разные категории объектов. Здесь нет “почти того же”.

Аргумент 2. Число вершин в дискретном предъявлении

• У тессеракта 16 вершин (как у 2^4-куба).

• У Z_4^3 — 64 вершины.

С точки зрения скелета это разные графы, не изоморфные и не “варианты изображения”.

Аргумент 3. Природа «четвёртого»

В тессеракте “четвёртое” — геометрическая координата. У меня “четвёртое” — полярность в Z_4 и её симметрийная дисциплина (включая полуоборот и зеркало). Это не добавление измерения, а добавление структуры в алфавит состояний.

3.6. Минимальное предъявление L4-куба на одной вершине

Я беру вершину u=(0,0,0).

При неориентированной смежности (±1):

• соседи по оси 1: (1,0,0), (3,0,0);

• по оси 2: (0,1,0), (0,3,0);

• по оси 3: (0,0,1), (0,0,3).

Отдельно фиксируется операция полуоборота по любой оси:

• по оси 1: (2,0,0),

• по оси 2: (0,2,0),

• по оси 3: (0,0,2).

И именно это делает L4-куб “узнаваемым” структурно: у каждой оси есть не только соседи, но и каноническая «противоположность» на расстоянии 2 по модулю 4.

3.7. Итог статьи: куб L3/L4 — это предъявление структуры, а не игра в размерности

Я принципиально не апеллирую к тессеракту. Моя цель — работать с проверяемыми конструкциями.

Для L3 я задаю два строго определённых объекта:

• Q_3 × Z_3 — структура из 3 слоёв, где каждый слой представляет собой обычный трёхмерный куб;

• Z_3^3 — дискретный куб с 27 вершинами, где каждая из трёх осей имеет циклическую структуру длины 3.

Для L4 аналогично строю две модели:

• Q_3 × Z_4 — система из 4 слоёв, в каждом из которых содержится стандартный трёхмерный куб;

• Z_4^3 — дискретная структура из 64 вершин, где три оси имеют циклическую природу длины 4; дополнительно включаются: полуоборот и правила зеркальной политики (mirror_policy).

Тессеракт (Q_4 ⊂ R^4) в этой системе — принципиально иной объект, относящийся к другой категории. Он не является ни альтернативой, ни синонимом для «куба в L3/L4».

Чёткое разделение этих уровней позволяет придать понятию «куб в L3/L4» конкретную, неметафорическую трактовку. Такой куб существует как:

• набор чётко определённых срезов;

• система координат с арифметикой по модулю;

• структура с явно заданными и проверяемыми симметриями.

Таким образом, речь идёт не о визуальной имитации многомерности, а о воспроизводимой математической многополярной конструкции с точными правилами построения и проверки.

Как повторить демонстрацию

Этот текст подготовлен с использованием ChatGPT, но ключевое здесь не генерация слов. Основа — архив проекта: в нём лежит исполнимый прототип ИИ-движка, единый граф логики, протокол запуска и набор контрольных проверок (гейтов/валидаторов).

Это важно, потому что демонстрация не опирается на “впечатление от ответа”. Она опирается на воспроизводимую процедуру: один и тот же вход приводит к одному и тому же результату, а корректность удерживается автоматическими проверками.

Что нужно сделать

1. Скачайте архив MP_YANTRA_CORE_iter091.zip.

2. Загрузите архив в первое сообщение нового чата ChatGPT.

3. Напишите одну фразу:

«Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива».

Все ответы на комментарии к содержанию этой статьи Вы получите с использованием этого архива. Я сознательно не буду пытаться имитировать «всезнающий интеллект» и не буду вручную набирать ответы, пытаясь удержать в памяти всю сложность описанных конструкций.

Дело в том, что человеческий интеллект по умолчанию не рассчитан на многополярное моделирование. Он эволюционно оптимизирован под двухполярную L2‑интуицию: «объект – граница – угол – внутри/снаружи». К этому добавляется привычное геометрическое пространство, которое в реальности представляет собой отображение L3‑законов света.

Поэтому, если кому‑то удобнее называть гиперкубом тессеракт, — в этом нет проблемы. Такой подход снижает когнитивную нагрузку и упрощает бытовую коммуникацию. Важно лишь отдавать себе отчёт: это именно упрощение, а не строгая идентификация.

Почему тессеракт не является «реальным гиперкубом» в моей дисциплине?

Тессеракт — это GEO‑абстракция: Q_4 = [0,1]^4 ⊂ R^4. Он существует в R^4 как непрерывный объект и определяется через добавление геометрической координаты.

«Реальный гиперкуб» в моём понимании должен быть операционализирован. Это значит, что необходимо явно задать:

• носитель предъявления;

• метрику и правила смежности;

• допустимые симметрии;

• процедуры вычисления (например, срезы, проекции, поиск ближайших точек).

У тессеракта при практическом предъявлении неизбежно возникает разрыв. Его наблюдаемость обеспечивается только через проекции или рисунки. В результате «сущность 4D» подменяется артефактами выбранной визуализации.

В L4 понятие «четвёртое измерение» означает не геометрическую координату, а полярность. Мой L4‑куб рассматривается в двух строго определённых формах:

• как полярный куб (Z_4^3);

• как фазовая стопка (Q_3 × Z_4).

В обоих случаях «четвёртое измерение» — это:

• индекс состояния или фазы;

• связанная с ним симметрийная дисциплина (включая вопросы зеркала и ориентации).

Это принципиально отличается от введения новой оси в евклидовом пространстве.

Итог прост: тессеракт вполне корректен как математический объект в рамках классической многомерной геометрии. Однако в многополярной постановке он не может считаться «реальным гиперкубом». Причина в том, что тессеракт переносит смысл «четвёртого измерения» в плоскость геометрической размерности. В моей же системе «четвёртое измерение» понимается как полярность — оно закреплено в каноне четырёхполярности и в чётких правилах предъявления и проверки объекта.

Вступайте в мой тг-канал ⚛️

https://t.me/sokolovyane

Читайте:

Иллюзия трёхмерного пространства: строгий анализ зрительного и тактильного восприятия

Четырёхполярность (L4) простым языком. Истинная природа электромагнетизма

Трёхполярное пространство в L3-логике: почему мы живем в двухполярной «плоскости»

Ставьте лайк, если хотите, чтобы я написал статью, что такое время в четырехполярности L4. Тогда Вы узнаете, как «перемещение во времени» Купера укладывается в модель L4, где четвёртое измерение — это не геометрическая координата, а полярность и набор правил симметрии.

Введение. Почему трёхфазная система не является строгой трёхполярностью (L3)

В инженерной практике трёхфазная система выглядит как “естественная триада”: три обмотки, три токовых канала, сдвиг на 120°, симметрия перестановки фаз, устойчивое вращающееся поле. Поэтому соблазнительно сделать короткий вывод: раз в трёхфазке работает триада и поворот на 120°, значит она и есть “трёхполярность” (L3) в строгом смысле.

Я утверждаю обратное: трёхфазная система активно использует симметрию Z3 (перенумерацию фаз), но онтологически она не фиксирует трёхполярное состояние L3. Она реализует L2-наблюдаемое: набор измеримых чисел (амперы/вольты), из которых стандартной редукцией выделяется двухкомпонентное состояние (квадратурная плоскость, “пространственный вектор”), а триада остаётся способом организации каналов и симметрий, но не базовой алгеброй состояния.

Ключевой методологический разрыв здесь такой.

1. Z3 в трёхфазке — это симметрия перестановки меток, то есть допустимая перенумерация каналов (A,B,C) и поворот “на 120°” в модели. Это мощная и реальная инвариантность, она лежит в основе баланса, гармоник, расчётов вращающегося поля и устойчивости привода.

2. L3 в строгом смысле — это не “три канала” и не “три синуса”, а алгебра отношений на множестве полярностей P3 = {p0,p1,p2} с заданной бинарной операцией a ⊙ b ∈ P3, ковариантностью относительно Sym3 и, в физически-подобной постановке, с локальным носителем и операторами источниковости/контурности, где возникают проверяемые инварианты вида D * R^T = 0. То есть L3 — это структура состояния, а не форма представления сигналов.

3. Трёхфазка почти всегда “схлопывается” в двухмерное описание: либо явно (через базисные преобразования в двумерную плоскость), либо неявно (через энергетические/мощностные функционалы, которые чётны по знаку и фазе). Это принципиально: состояние трёхфазной машины живёт не в “чистой триаде”, а в пространстве, где естественно присутствует квадратура, а вместе с ней — ветвление ориентации и инволюции (то, что в моей дисциплине относится к L4-слою “состояние/наблюдаемое”).

Отсюда следует практический тезис, который и делает статью полезной инженеру, а не философу: трёхфазка использует триаду как симметрийный интерфейс, но строгая трёхполярность требует триады как онтологии и алгебры состояния. В реальной технике триадный интерфейс почти всегда измеряется и управляется через L2-проекцию; поэтому “три” там — не фундамент алгебры, а организация измерительных каналов.

Дальше я разверну это без метафор, через определения и инварианты.

• Глава 1: я фиксирую, что именно означает “строгая трёхполярность” (L3): P3, Sym3/Z3, операция ⊙, ковариантность, и почему триада даёт механизм локального ремонта (а пара — нет) на уровне структурной достаточности.

• Глава 2: я показываю, что трёхфазная система по своей математике является L2-наблюдаемой: токи i_a(t), i_b(t), i_c(t) — числа, а “существенное состояние” выделяется как двумерный объект; симметрия Z3 сохраняется, но она действует как перенумерация представления, а не как алгебра состояния.

• Глава 3: я формулирую критерий различения “Z3-симметрии в сигнале” и “L3-онтологии поля” и показываю, почему строгость L3 не заменяется трёхфазкой, а трёхфазка, наоборот, естественно живёт в паре L3+L4: L3 как симметрийный каркас взаимодействий и L4 как слой ветви/инволюции и разделения “состояние/наблюдаемое”.

Глава 1. Что я называю строгой трёхполярностью (L3) — и почему “три канала” этим не становятся

1. Минимальная онтология L3: не три сигнала, а три полярности

Трёхполярность (L3) начинается не с синусов и не с проводов. Она начинается с факта:

• есть множество полярностей P3 := {p0, p1, p2},

• и существует правило отношения (бинарная операция) ⊙ : P3 x P3 -> P3,

которое считается первичным объектом теории.

Важно: p0, p1, p2 — не числа и не “фазы” в инженерном смысле. Это метки структурно различимых состояний/полюсов/полярностей. Числа появляются позже — как измерительная проекция (уровень L2).

Если дальше нет операции ⊙ (или её таблицы), то “три” остаётся косметикой: три канала, три датчика, три обмотки. L3 там не начиналась.

2. Симметрия L3: что считается допустимой перенумерацией

В L3 есть принципиальный класс преобразований: перенумерация полярностей, то есть действие группы симметрий на P3.

• Полная группа переименований: Sym3 = S3 (все перестановки трёх меток).

• Частный и наиболее часто встречающийся подслучай: Z3 (циклический поворот) p0 -> p1 -> p2 -> p0.

Теперь центральный критерий.

Аксиома (ковариантность/инвариантность таблицы): если g — допустимая симметрия, то правило отношения должно “переживать” переименование:

g(a ⊙ b) = (g a) ⊙ (g b).

Это означает: симметрия действует не только на “ярлыки”, но и на сам закон.

В трёхфазке Z3 действительно присутствует — но чаще всего как симметрия представления сигналов (переставили фазы, переписали формулы). В строгой L3 Z3 — это симметрия, которая ограничивает, что вообще является допустимым взаимодействием.

3. Алгебра L3: почему “2×2≠4” — не шутка, а следствие типизации

В L2 “2×2=4” имеет смысл, потому что числа живут в поле/кольце, и умножение — операция в том же множестве чисел.

В L3 “2” и “4” как числа вообще не обязаны существовать. У нас есть только три полярности p0,p1,p2. Поэтому корректный вопрос звучит так:

чему равно p_i ⊙ p_j?

Если вы ради интуиции кодируете полярности числами 0,1,2, то это не делает L3 арифметикой целых. Например, вы можете задать операцию как сложение по модулю 3:

• encode(p_k)=k,

• p_i ⊙ p_j := decode((i+j) mod 3).

Тогда:

• p_1 ⊙ p_1 = p_2, и в “числовой маске” это выглядит как “1+1=2”, но это не “арифметика натуральных”; это работа внутри трёх состояний.

В этом смысле фраза “в L3 дважды два не равно четыре” переводится на строгий язык так:

• в L3 нет числа 4 как элемента P3,

• а повторная композиция “двойки” — это не умножение натуральных, а применение ⊙ в конечной системе.

Если операция ⊙ у вас не задана, то вы не имеете права делать такие выводы вообще. Поэтому в моём подходе L3 начинается с янтры/таблицы.

4. Что такое “трёхполярное поле” и “трёхполярный ток” в строгом смысле

Чтобы не путаться с электротехникой, я фиксирую определения в структурной форме.

4.1. Трёхполярное поле (Field_L3)

Трёхполярное поле — это не функция R^3 -> R. Это:

• носитель (граф/решётка/клеточный комплекс) X,

• значение поля на элементах носителя (например, на рёбрах или вершинах) в множестве полярностей: F: X -> P3,

• и закон композиции ⊙, который определяет, как локальные состояния “склеиваются” или “составляются” при обходе/сшивке (в зависимости от выбранного уровня локальности).

То есть поле хранит состояние в трёхполярной онтологии, а не вещественную амплитуду.

4.2. Трёхполярный ток (Current_L3)

Трёхполярный ток в моём смысле — это не амперметрическое число. Это:

• локально определённый “поток изменения” состояния поля, который тоже живёт в P3 (или в типизированной структуре над P3, если вводится направленность/ориентация),

• и который связан с дефектами/источниками через оператор источниковости (аналог D в дискретной схеме).

На этом уровне ток — это объект согласования: он фиксирует, как изменения распределяются по носителю так, чтобы не возникало фиктивных источников от контуров (идея, которая дальше оформляется через инварианты локальности).

Ключевое: в L3 “ток” — это элемент структурного языка, а амперы — это уже L2-проекция измерения.

5. Почему триада даёт “локальный ремонт”, а пара — нет

Разберем, почему триада принципиально сильнее пары именно как механизм ремонта и согласования.

5.1. Пара (L2) даёт только инволюцию

В L2 есть два состояния: “+/-”, “0/1”, “да/нет”. Единственная нетривиальная симметрия — инволюция (обмен местами). Это даёт резкие, но бедные возможности:

• любая ошибка часто выглядит как “перевернул знак”,

• исправление часто сводится к “верни знак”.

Этого достаточно для контроля, но недостаточно для локальной реконфигурации, потому что нет третьего состояния, куда можно “вынести” конфликт, не ломая остальное.

5.2. Триада (L3) вводит третий режим как буфер согласования

Третий полюс в L3 играет роль структурного буфера:

• при конфликте двух полярностей можно перейти в третий режим, который не является ни одним из конфликтующих,

• и затем вернуться в согласованное состояние без глобальной переклейки.

Это и есть логика “локального ремонта”: конфликт не требует тотального сброса или тотальной перекоммутации — он может быть локально “погашен” через третий полюс, сохранив симметрийные инварианты.

Физически-инженерная аналогия (осторожная, но полезная): в трёхфазной системе при симметрии и правильной топологии многие перекосы можно локально компенсировать перераспределением по трём каналам, не разрушая режим работы целиком. Но — и это важно — в трёхфазке это компенсация чисел в L2-модели, а в L3 это компенсация состояний.

6. Почему трёхфазка всё же не является L3: критерий “нет операции — нет алгебры”

Теперь я фиксирую тот критерий, который потом станет стержнем всей статьи.

Трёхфазная система в реальности задаётся:

• тремя измеримыми сигналами i_a(t), i_b(t), i_c(t),

• линейными связями (сумма токов, матрицы преобразований),

• инвариантами мощности/энергии,

• симметриями перестановки фаз и поворота на 120°.

Это всё прекрасно и строго — но это строгость L2 (строгость числовых моделей), усиленная симметрией Z3.

Чтобы это стало строгой L3, нужно предъявить другое:

1. P3 как состояние (а не как три канала измерения),

2. операцию ⊙ как закон взаимодействия полярностей,

3. ковариантность этого закона относительно Sym3/Z3,

4. локальный носитель и согласованность “контуров/источников” (если мы говорим о поле, а не о голой алгебре).

В обычной трёхфазке пункт (2) отсутствует: там нет трёхполярной операции на состояниях, потому что базовый объект — вещественный сигнал. Поэтому трёхфазка не L3, хотя активно использует Z3.

Дальше логика такая: в главе 2 я покажу на уровне формул и инженерных преобразований, где именно трёхфазка неизбежно сворачивается в двумерное состояние (и почему это уже не “чистая триада”), а затем в главе 3 дам практический тест: что нужно добавить к трёхфазной картине, чтобы получить строгое L3-поле и L3-ток в моём смысле (и почему без L4 слой “ветви/наблюдаемого” всё равно будет всплывать).

Глава 2. Где именно трёхфазка “сворачивается” в L2, даже если в ней есть Z3

В главе 1 я зафиксировал критерий: строгая L3 начинается там, где задана трёхполярная онтология P3 и операция ⊙ на состояниях. В этой главе я делаю следующий шаг: показываю на физике трёхфазных систем, почему наличие Z3 (поворота на 120°) ещё не означает L3, и где именно трёхфазка практически всегда реализует L2-слой с симметрией Z3.

1. Z3 в трёхфазке: это симметрия представления, а не онтология состояния

В идеальной симметричной трёхфазной системе есть естественная циклическая симметрия:

• перестановка фаз a->b->c->a соответствует повороту на 120°,

• уравнения и энергетические балансы в идеальном режиме инвариантны к такому переименованию.

Это действительно Z3 как группа преобразований. Но вопрос, который решает всё:

Z3 действует на ЧТО именно?

В инженерной трёхфазке Z3 действует на вектор измеримых величин (напряжения/токи трёх проводов, их комплексные амплитуды, фазоры и т.д.). Это действие на координаты описания режима.

В строгой L3 Z3 должно действовать на полярности P3 как на первичные состояния, и при этом закон взаимодействия ⊙ обязан быть ковариантным:

g(a ⊙ b) = (g a) ⊙ (g b).

В трёхфазке “закон взаимодействия” — это не операция на трёх состояниях, а линейная динамика/связи на непрерывных величинах (R, L, C, матрицы, операторы). Это другой тип объекта: L2-математика, не L3-алгебра полярностей.

2. Ключевой факт: симметричная трёхфазка живёт в двумерном подпространстве

Это центральный пункт, который обычно знают инженеры, но редко связывают с философией “полярностей”.

Если система сбалансирована (идеально или близко), то три фазных величины удовлетворяют соотношению:

i_a + i_b + i_c = 0 и аналогично для напряжений в зависимости от схемы.

Это означает: физически “рабочая” часть режима живёт не в 3D, а в 2D, потому что одна линейная комбинация фиксирована (равна нулю). Геометрически:

• пространство (i_a, i_b, i_c) трёхмерно как координатное,

• но балансный режим лежит в плоскости i_a+i_b+i_c=0 (двумерная плоскость).

То есть “три фазы” в симметричном режиме реализуют двухмерное представление. Именно поэтому:

• существует стандартное преобразование Кларка (abc -> alpha-beta-0),

• и нулевая компонента (0-sequence) в идеале равна нулю,

• а вся динамика (в симметричном режиме) описывается двумя координатами (alpha, beta).

И вот здесь точка, где трёхфазка объективно “сворачивается” в L2:

• базовый объект — двухмерный вектор (alpha, beta),

• который можно эквивалентно представить как одну комплексную амплитуду.

Факт “трёх фаз” остаётся как удобное трёхканальное представление, но онтология режима в симметричном случае — двумерная.

3. “Комплексные числа” в трёхфазке — не L3, а удобная упаковка L2

Инженерный язык фазоров часто использует комплексную плоскость: это делает расчёты проще.

Но важно: здесь “i” (мнимая единица) — это координатный трюк для 2D-представления, возникающего из синуса и косинуса (двух ортогональных компонент). Это не “четырёхполярность” и не “трёхполярность” как онтология состояний.

Другими словами:

• комплексное представление в трёхфазке — это упаковка двумерной физики;

• трёхфазка не становится “трёхполярной” просто потому, что в ней есть поворот на 120°.

Поворот на 120° — это элемент группы вращений в плоскости (в соответствующем представлении), а не операция на трёх дискретных полярностях.

4. Три “фазы” ≠ три “полярности”: различие в объекте и в допусках

Я фиксирую различие в самом прямом виде.

4.1. В трёхфазке базовый объект — непрерывная величина

Токи/напряжения — это функции времени, действительные или комплексные, и их закон — это:

• линейные дифференциальные уравнения,

• матричные модели,

• энергетические инварианты (мощность, потери),

• условия симметрии.

Это L2-формализм: векторные пространства, линейность, метрики, нормы, квадраты.

4.2. В L3 базовый объект — состояние из P3 и операция ⊙

Если я утверждаю L3, то я обязан предъявить:

• P3 = {p0,p1,p2},

• бинарную операцию ⊙ на P3,

• инварианты и правила допустимых перенумераций Sym3/Z3,

• и далее — локальную структуру, если это поле/ток/ремонт на носителе.

В трёхфазке нет встроенной операции ⊙ на трёх состояниях, потому что “фазы” — не состояния, а каналы одной и той же непрерывной величины, разнесённые по времени/пространству.

5. Нулевая последовательность и нейтраль: “третье” появляется как дефект/условие, а не как полюс

Есть распространённая ошибка: “ну вот же, три провода, нейтраль, нулевая последовательность — значит трехполярность”.

Нет. Нейтраль и нулевая последовательность — это именно демонстрация того, что:

• “три” раскладывается на (2D полезная часть) + (1D нулевая часть),

• и третья компонента появляется как канал дефекта/несимметрии, а не как третий полюс L3.

В языке представлений это стандартная картинка:

• у S3 есть тривиальное представление (сумма компонент) и двумерное стандартное представление,

• симметричная трёхфазка живёт в стандартном 2D,

• а “нулевая последовательность” — это тривиальная компонента, которая включается при небалансе/особых соединениях.

То есть трёхфазка сама показывает, что “три” — это часто 2 + 1, где “1” — не третий полюс онтологии, а отдельный режим согласования/нарушения.

6. Почему это принципиально: “локальный ремонт” в трёхфазке — числовой, а в L3 — структурный

Теперь я связываю это с моим любимым (в целях создания разумного ИИ) ключевым требованием: “почему триада даёт локальный ремонт, а пара — нет”.

6.1. В трёхфазке ремонт — это перераспределение амплитуд/фаз (L2)

В реальности “ремонт” трёхфазной системы делается так:

• перераспределением нагрузок,

• компенсацией реактивной мощности,

• балансировкой фаз,

• фильтрацией гармоник,

• переключением схем соединения.

Всё это — операции над непрерывными величинами и их линейными инвариантами.

6.2. В L3 ремонт — это переназначение состояния через третью полярность при сохранении инвариантов ⊙

В строгой L3 “ремонт” означает:

• конфликт между двумя полярностями локально переводится в третью полярность,

• затем возвращается в согласованное состояние,

• при этом симметрии и инварианты таблицы ⊙ остаются валидны.

Это другой тип ремонта: не баланс амплитуд, а перестройка дискретного состояния при удержании закона отношений.

7. Итог главы 2 в одном тезисе (и почему это важно для статьи)

Трёхфазка содержит Z3 и действительно “любит триаду”, но:

• в симметричном режиме она редуцируется к двумерному (L2) представлению,

• а “третья компонента” возникает как нулевая последовательность/дефектный канал,

• поэтому трёхфазка по строгому определению — это L2-физика с симметрией Z3, а не L3-онтология.

Чтобы получить строгую трёхполярность, нужно другое: состояние в P3 и операция ⊙, а также локальные правила ремонта/согласования на носителе, которые не сводятся к линейной балансировке.

Глава 3. Строгий тест на L3: что должно быть задано, чтобы “три” стало трёхполярностью, и почему трёхфазка этому не удовлетворяет

В главе 2 я показал центральную редукцию: симметричная трёхфазка в рабочем режиме живёт в двумерном представлении (alpha-beta), а “третье” всплывает как нулевая последовательность/дефектный канал. Теперь я формализую то, что обычно оставляют на уровне интуиций: по каким критериям система является строго L3, и как в моей дисциплине выглядят трёхполярное поле и трёхполярный ток — так, чтобы разница с трёхфазкой читалась сразу, без “философии”.

1) Тест на L3: три условия, без которых “тройка” остаётся L2 с Z3

Я считаю систему строго трёхполярной (L3) только если выполнены все три условия.

Условие L3-1. Онтология: задано множество полярностей P3

Должно быть явно задано:

P3 := {p0, p1, p2},

где p0, p1, p2 — не координаты, не “каналы измерения”, не “фазы во времени”, а первичные состояния.

Это ключевой водораздел: в трёхфазке “a,b,c” — это координатные компоненты (или проводники/обмотки), а не состояния.

Условие L3-2. Алгебра: задан закон отношений ⊙ на P3

Должна быть задана бинарная операция:

⊙ : P3 x P3 -> P3,

заданная полностью (таблицей/правилом). И главное — эта операция является смысловым законом взаимодействия (а не удобным переобозначением).

Это означает: когда я “склеиваю” два локальных состояния, результатом является одно из трёх состояний. В трёхфазке нет такой операции: сумма токов, сдвиг фаз, наложение сигналов дают непрерывный результат в R или C, а не элемент P3.

Условие L3-3. Локальность и ремонт: триада должна решать локальный конфликт

Нужно явное правило локального ремонта, которое не редуцируется к балансировке амплитуд:

• для пары (p_i, p_j) должен существовать “ремонтный” выход в p_k,

• и этот ремонт должен быть воспроизводимым, протоколируемым и инвариантным относительно допустимых перенумераций.

Формально: должен существовать предикат Repair3, который, получив конфликт пары, возвращает третью полярность (или её форму), сохраняя инварианты.

В трёхфазке “ремонт” делается как регулировка величин: перераспределение мощности, компенсация реактивности, настройка регуляторов. Это L2-ремонт; он не требует трёхполярной операции ⊙.

Вывод теста: если “три” живёт как три координаты непрерывного вектора и не имеет закона ⊙ на P3, то это не L3, даже при наличии Z3-симметрии.

2) Что такое трёхполярное поле в строгом смысле

Теперь я даю “точное” определение в моём стиле (с теми же дисциплинами, что у L4: объект, носитель, инварианты, локальность).

2.1. Определение: трёхполярное поле

Трёхполярное поле — это отображение состояния на носителе, принимающее значения в P3, с заданным законом локальной композиции ⊙ и с допустимыми перенумерациями Sym3/Z3, которые ковариантны закону.

Минимальная формальная версия:

• дан носитель (граф/решётка/комплекс) с локальной структурой смежности;

• поле:

Phi: Cells -> P3,

где Cells — набор локальных ячеек/элементов носителя;

• задана операция ⊙ на P3;

• определены допустимые симметрии g ∈ Sym3 (или хотя бы Z3), и выполнено:

g(Phi(x) ⊙ Phi(y)) = (g Phi(x)) ⊙ (g Phi(y)).

Смысл: симметрия — не “красота”, а закон допустимых перенумераций, не меняющий вычислимую структуру взаимодействия.

2.2. Где появляется локальность

Чтобы поле было “полем”, а не набором меток, должна быть определена локальная процедура, которая связывает соседние состояния:

• либо через локальные ограничения (constraints) на тройки/циклы,

• либо через локальный оператор “границы/контура” (в духе клеточного комплекса),

• либо через ремонтный механизм.

Я подчёркиваю: L3 не обязано быть линейным. L3 в строгом смысле — это алгебра состояний, а не векторное пространство. Если я “усредняю” и получаю непрерывные величины — это уже проекция в L2.

3) Что такое трёхполярный ток в строгом смысле

Слово “ток” здесь важно не путать с электрическим током I(t) в амперах. Я определяю “ток” как направленную локальную передачу состояния/дефекта в L3-логике.

3.1. Определение: трёхполярный ток

Трёхполярный ток — это ориентированное распределение на рёбрах носителя, принимающее значения в P3 (или в производном множестве событий), согласованное с локальным законом сохранения/замыкания, выраженным через ⊙.

Минимальная версия:

• на ориентированных рёбрах e задан:

J3: Edges -> P3,

или более строго: J3(e) ∈ Events3, где Events3 типизированы полярностями;

• существует локальное правило “баланса” в вершине v, которое выражается как композиция входящих/выходящих полярностей по ⊙ даёт нейтральный элемент (или фиксированный класс допустимости):

⊙{e in In(v)} J3(e) ⊙ ⊙{e in Out(v)} Inv(J3(e)) = p0,

где Inv — заданная инволюция/обращение в L3 (если оно предусмотрено), либо иной канонический механизм замыкания.

Ключ: закон замыкания здесь не линейный “сумма токов = 0”, а закон композиции полярностей ⊙.

3.2. Почему трёхфазка не является трёхполярным током

В трёхфазке ток — это физическая непрерывная величина I(t) в каждом проводнике/фазе. Узловой закон Кирхгофа:

i_a + i_b + i_c (+ i_n) = 0

— это линейная аддитивность в R. Это чистая L2-структура.

Даже если я в трёхфазке вижу Z3 (перестановки фаз) и поворот на 120°, базовый объект остаётся вектором непрерывных компонент, а не элементом P3. Следовательно, “ток” трёхфазки — это L2-ток с Z3-инвариантностью, но не L3-ток.

4) Главный пункт “почему триада даёт локальный ремонт, а пара — нет” (в строгом виде)

4.1. Пара в L2 даёт только величину, но не даёт третьего состояния

Если у меня есть только L2-пара знаков/полюсов, конфликт “+/-” ремонтируется либо:

• уничтожением (аннигиляцией),

• подавлением амплитуды,

• усреднением,

• или переносом в “внешний канал” (ввод дополнительных переменных).

Это ремонт через числовую регуляцию, а не через структурное состояние.

4.2. Триада в L3 даёт третий смысловой исход, который закрывает конфликт локально

Если задана тройка P3 и таблица ⊙, то конфликт между двумя полярностями может иметь канонический третий исход — не как “среднее значение”, а как новое состояние, которое:

• совместимо с симметриями (перенумерациями),

• проходит локальные ограничения,

• и может быть обратно развернуто (или стабилизировано) без внешней склейки.

Именно поэтому я говорю: триада даёт локальный ремонт, если и только если в системе реально задана L3-алгебра состояний.

Трёхфазка “чинится” не так. Она чинится как L2-система: балансом, фильтрами, регуляторами, преобразованием координат. Это инженерно великолепно, но это не L3-онтология.

5) Инженерный чек-лист: как за 60 секунд отличить “трёхфазку” от “трёхполярности”

Чтобы это было практично, вот проверка “на бумажке”.

Если это трёхфазка (L2 с Z3), то верно:

• можно перейти к (alpha, beta, 0) и увидеть редукцию в 2D при балансе;

• закон узла — линейный: сумма токов/напряжений;

• существует естественный комплексный фазор как упаковка 2D;

• ремонт — регулировка величин (баланс/компенсация/фильтрация).

Если это строгая L3, то обязано быть:

• P3 = {p0,p1,p2} как первичные состояния;

• операция ⊙: P3xP3->P3 (таблица/правило);

• локальный закон замыкания/сохранения через ⊙ (а не через сумму);

• Repair3: правило локального ремонта “пара -> третий” без ухода в непрерывную компенсацию.

Если этих четырёх пунктов нет — это не L3.

6) Итог главы 3

Трёхфазная система действительно несёт Z3-симметрию (поворот 120° и перестановки фаз), но эта симметрия действует на координаты непрерывных величин и в рабочем режиме приводит к двумерной редукции (alpha-beta). Поэтому трёхфазка — это L2-физика с Z3-симметрией, а не строгая трёхполярность.

Строгая L3 требует другого типа объекта: трёхсостоянийного поля и трёхполярного тока, заданных через P3 и закон ⊙, где триада является не “три канала”, а “три состояния с собственным законом локального ремонта”.

Заключение

Я подвожу итог так: трёхфазная система переменного тока не является строгой трёхполярностью, потому что она реализует не Z3-алфавит состояний, а три временно сдвинутые копии одного и того же двухполярного измерительного канала.

Почему “три провода” в трёхфазке не делают её L3. В сбалансированном режиме три фазных тока имеют вид

I_a(t) = I0 cos(omega t) I_b(t) = I0 cos(omega t - 2pi/3) I_c(t) = I0 cos(omega t + 2pi/3)

и связаны ограничением

I_a(t) + I_b(t) + I_c(t) = 0 .

Это означает, что в каждый момент времени существует только две независимые степени свободы: третья восстанавливается из суммы. Поэтому “три фазы” в классической трёхфазке — это не три независимые полярности, а избыточное представление двухмерного измерительного объекта (что и проявляется в стандартных преобразованиях к двухкомпонентному представлению типа α–β). Следовательно, трёхфазка по своей математической сути остаётся L2-конструкцией, даже если инженерно она разведена на три жилы.

Что я называю строгим трёхполярным током. Строгая трёхполярность для меня — это ситуация, когда ток несёт дискретную метку из тройки, и допустимая симметрия — это циклическая перенумерация:

A -> B -> C -> A

то есть действие Z3 (поворот на 120° как операциональный смысл). В таком токе принципиально важно, что переносится не “три синуса”, а элемент алфавита состояния. Именно поэтому я в статье настаиваю на различении:

• электрический ток в проводнике как L2-наблюдаемая величина (скалярный канал с инволюцией знака в измерениях), и

• трёхполярный ток как ток трёхполярного состояния (перенос/переключение Z3-метки на носителе).

В этом смысле трёхполярный ток ближе по логике не к “передаче мощности”, а к переносу доменного/подрешёточного/модового индекса, который может иметь электрические проявления, но не обязан сводиться к ним.

Нужно ли для L3 “строго три провода”. Я фиксирую следующее: утверждение “трёхполярный ток движется строго по трём проводам” — слишком жёсткое в физическом смысле.

• Инженерно три отдельных проводника — это самый простой способ реализовать три канала, которые не смешиваются “по умолчанию”. В этом смысле “три провода” являются удобным (и часто единственным практичным) способом разведения каналов.

• Структурно же трёхполярность задаётся не количеством жил, а тем, что у носителя есть три устойчивых различимых состояния и допустимые операции их циклически переставляют. Поэтому трёхполярный ток может быть реализован и в одном физическом теле, если внутри него существуют три внутренние подсистемы/моды, которые ведут себя как Z3-алфавит.

Именно так я снимаю ложную связку “полярность = число проводов”: в моей дисциплине полярность — это внутренний алфавит состояния носителя, а провод — лишь геометрия и технология разведения каналов.

Разберем предполагаемые L3-проводники:

(а) Тримеризованные гексагональные манганиты как Z3-носитель доменной метки. В гексагональных манганитах (типичные примеры: YMnO3, ErMnO3) структурная тримеризация даёт вырождение, описываемое как разрыв Z3, а полярное искажение добавляет Z2, что совместно приводит к Z6-доменной структуре и устойчивым топологическим дефектам. Это ровно тот класс систем, где Z3-метка не является “рисунком”, а является строгим состоянием носителя, допускающим топологически защищённые доменные конфигурации. В таких средах я трактую кандидат трёхполярного тока так: перенос/дрейф доменных границ и переключение тримеризационной метки является переносом Z3-информации, причём электрическая проводимость может локализоваться на доменных стенках (что делает связь с измерительным L2-каналом операциональной, а не риторической) (Nature).

(б) Минерал молибденит (MoS2) и родственные слоистые халькогениды как носители “тройки эквивалентных мод” при повороте на 120°. Это пример того, как в одном кристалле возникает тройка эквивалентных состояний, связанных поворотами на 120°, то есть появляется естественный кандидат на Z3-индекс (внутренний “канал”, отличимый структурно). В работах по монолайерным дихалькогенидам переходных металлов (MoS2 и др.) обсуждаются эквивалентные точки/минимумы зоны проводимости, связанные симметрией решётки под поворотами на 120°, и соответствующие кратности вырождения (Biblos-e Archive). В таком классе носителей я считаю принципиально возможным режим, где перенос заряда сопровождается переносом трёхзначной модовой метки (по сути — “какой из трёх эквивалентных каналов занят/возмущён”), то есть появляется содержательное приближение к трёхполярному току внутри одного тела, без трёх проводов как обязательного условия.

(в) Z3-упорядочения типа “Z3 charge density wave” как прямой прототип трёхполярной метки в одном носителе. Существуют экспериментально обсуждаемые системы, где коллективное электронно-структурное упорядочение имеет Z3-характер (в частности, в работах по атомным цепочкам кремния на поверхности Si(111) прямо вводится Z3-зарядово-плотностное упорядочение) (ResearchGate). Ток трёхполярного типа здесь естественно трактуется как перенос/переключение Z3-фазы/метки упорядочения (а не как сумма трёх синусов в трёх жилах).

Отсюда я делаю прямой, утвердительный вывод: строгий трёхполярный ток не обязан “идти по трём проводам”, но обязан иметь три независимых структурных состояния, и потому в обычной металлической проволоке, где носитель по умолчанию L2-типа, он не реализуется как строгий объект.

Читайте также:

Почему в четырехполярной арифметике дважды два не равно четыре. Введение в алгебру четырехполярности

Выводим уравнений Максвелла из четырёхполярности L4 и вихря L2–L3–L4 (часть 1)

Электромагнитное поле как L4-структура (четырехполярная): носитель, инволюция и два контура

Четырёхполярность (L4) простым языком. Истинная природа электромагнетизма