Выбор оптимального метода решения СЛАУ на основе анализа датасета
Полное руководство по выбору алгоритма для систем линейных уравнений
Меня зовут Руслан Сенаторов, я занимаюсь математическим обоснованием машинного обучения.
В этой статье, я расскажу как выбрать метод для определённого типа датасета, чтобы ваш код работал быстро, точно и без ошибок? И вы получили премию от руководства!
Введение
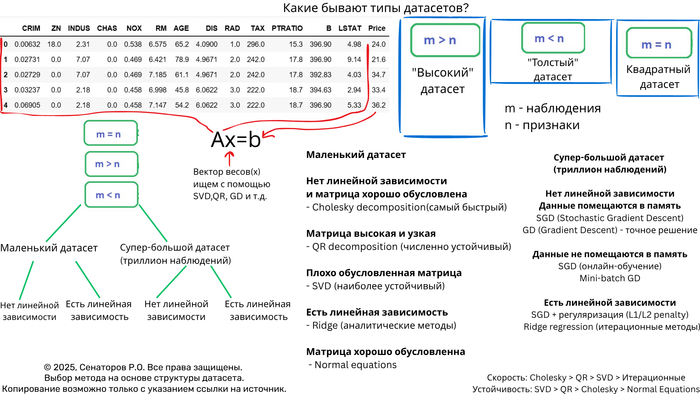
Решение систем линейных уравнений (СЛАУ) вида Ax = b — фундаментальная задача вычислительной математики и машинного обучения. Однако универсального метода не существует — выбор алгоритма критически зависит от характеристик датасета. Неправильный выбор может привести к катастрофическому замедлению вычислений или полной потере точности.
Ключевые характеристики датасета
1. Размер и структура матрицы
n_samples × n_features — соотношение наблюдений и признаков
Плотность/разреженность — процент ненулевых элементов
Обусловленность — число обусловленности матрицы
2. Вычислительные ограничения
Объем оперативной памяти
Требования к точности
Время вычислений
Дерево решений для выбора метода
Маленькие датасеты (n < 1000)
Плотные хорошо обусловленные матрицы
# Холецкий — самый быстрый для POSDEF матриц
if np.all(np.linalg.eigvals(A) > 0):
L = np.linalg.cholesky(A)
x = solve_triangular(L.T, solve_triangular(L, b, lower=True))
Матрицы общего вида
# QR-разложение — золотой стандарт
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
Плохо обусловленные системы
# SVD — максимальная устойчивость
U, s, Vt = np.linalg.svd(A, full_matrices=False)
x = Vt.T @ np.diag(1/s) @ U.T @ b
***
Средние датасеты (1000 < n < 10,000)
"Высокие" матрицы (n_samples >> n_features)
# QR остается оптимальным
# Сложность O(mn²) эффективна при m >> n
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
"Широкие" матрицы (n_samples << n_features)
# Итерационные методы или регуляризация
from sklearn.linear_model import Ridge
model = Ridge(alpha=1e-6, solver='lsqr')
model.fit(A, b)
x = model.coef_
***
Большие датасеты (n > 10,000)
Разреженные матрицы
# Итерационные методы
from scipy.sparse.linalg import lsqr
x = lsqr(A, b, iter_lim=1000)[0]
***
Огромные датасеты (n > 1,000,000)
Стохастические методы
from sklearn.linear_model import SGDRegressor
model = SGDRegressor(max_iter=1000, tol=1e-3)
model.fit(A_batches, b_batches) # Мини-батчи
Когда использовать нормальные уравнения?
"Высокие" матрицы (m >> n)
# Решение через нормальные уравнения
x = np.linalg.inv(A.T @ A) @ A.T @ b
# Или более устойчивый вариант
x = np.linalg.solve(A.T @ A, A.T @ b)
10000 наблюдений и 50 фитч - Идеально для нормальных уравнений
cond_number = np.linalg.cond(A.T @ A) # < 10^8 Хорошо обусловленная
Детальный анализ методов
Точные методы (прямые)
Итерационные методы
SGD | Подходит для огромных данных | Медленная сходимость
Заключение
Выбор оптимального метода решения СЛАУ — это искусство баланса между точностью, скоростью и требованиями к памяти. Ключевые рекомендации:
Маленькие матрицы → Прямые методы (QR/SVD)
Большие разреженные → Специализированные разреженные решатели
Огромные плотные → Итерационные методы с предобуславливанием
Экстремальные размеры → Стохастическая оптимизация
Главное правило: Всегда начинайте с анализа структуры и свойств вашей матрицы — это сэкономит часы вычислений и предотвратит численные катастрофы.
Используйте это руководство как отправную точку для выбора оптимального стратегии решения ваших задач линейной алгебры.