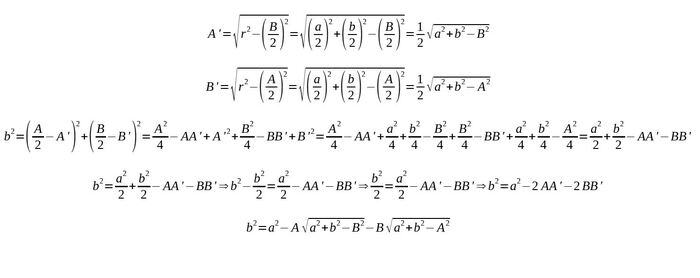К сожалению в своём решении нашёл ошибку и забросил это дело. Но теперь вернулся. Посмотрите, с картинками и формулами сделал. Есть ли ошибки?
В результате уравнение получилось, но с одной переменной.
Вопрос вписывания прямоугольника в прямоугольник "впритык" (решение вопроса-поста)
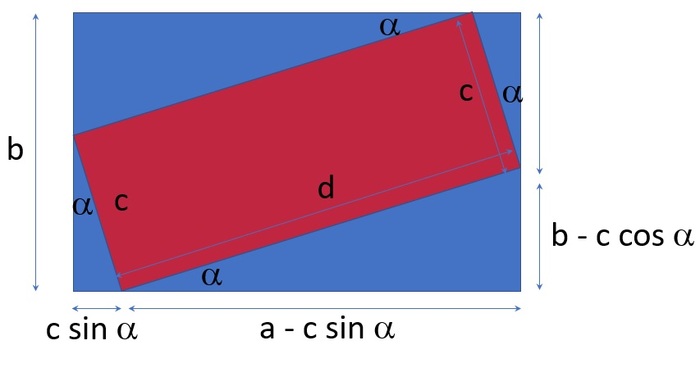
Пусть a — ширина основного прямоугольника, b — длина основного прямоугольника, c — ширина вписываемого прямоугольника и d — длина вписываемого прямоугольника (неизвестно), α — угол наклона (неизвестно).
Вписываемый прямоугольник лежит на сторонах основного прямоугольника.
Частная задача (в посте-вопросе): максимум длины вписываемого прямоугольника (по размерам основного и ширине вписанного прямоугольника).
Общая задача: найти по имеющимся нескольким значениям другие значения.
ОБЩЕЕ РЕШЕНИЕ
1. Как найти длину вписанного прямоугольника по формуле, при a=4; b=3; c=1 (в один клик):
Ответ: d≈4.0851, α≈31.7501
Инструмент ищет угол наклона/любую сторону, если есть 3 из 5 показателей
(вставьте свои значения вместо a, b, c, d, α)!
2. Подробное описание решения (методом Крамера и матрицами):
3. Решение, предложенное @vardader (#comment_364405448), кстати, верное (обратные знаки, на нахождение корней не влияет). При a=4; b=3; c=1:
Выходит четыре ответа, из них только одно действительное, а остальные отрицательные и комплексные: d≈4.0851, α≈31.7501
Справочно:
4. До угла в градусах
α = arctan((a*c-b*d)/(b*c-a*d))*180/π
дошли так.
1) Известно (система уравнений):
d*сos(α)+c*sin(α)=a
c*cos(α)+d*sin(α)=b
2) Перемножаем крест накрест:
b*(d*сos(α)+c*sin(α)) = a*(c*cos(α)+d*sin(α))
3) Раз мы знаем, что tg(α) = sin(α)/cos(α), то делим обе части уравнения на cos(α):
b*d+b*c*tg(α) = a*c+a*d*tg(α)
4) Переносим часть с тангенсом в одну сторону, выносим его за скобки, выражаем его отдельно:
b*c*tg(α) - a*d*tg(α) = a*c - b*d
tg(α) (b*c - a*d) = a*c - b*d
tg(α) = (a*c - b*d) / (b*c - a*d)
5) Из численного значения tg(α) получить
- радианы можно через арктангенс, или единица делить на тангенс: 1/tg(α)=arctan(α),
- градусы можно при домножении ещё на 180/π: arctan(α)*180/π
Таким образом, угол наклона в градусах:
α = arctan((a*c-b*d)/(b*c-a*d))*180/π
Справочно:
5. Ещё смежные вопросы рассматривались здесь
#comment_364391099
Теперь с помощью этого инструмента Wolfram Alplha, имея три стороны двух прямоугольников, можно находить четвёртую недостающую и угол наклона!
В том числе, имея a, b, c, можно находить длину d вписываемого прямоугольника, в чём и был вопрос.
Проблема решена
А у меня вот прикладная задачка по геометрии.
Неоднократно сталкивался на практике, так и не придумал, как точно на аналитически найти ответ. Программы умеют это делать, а вот как посчитать - хз.
Подозреваю, что способ решения может быть связан с пределами или интегралами, геометрически или тригонометрически посчитать не сумел.
Дано...
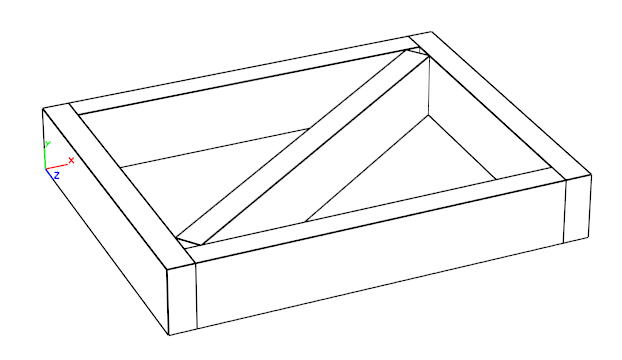
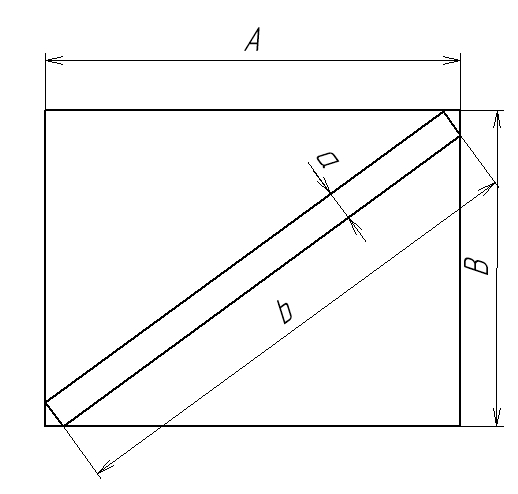
Ну, чтоб было понятно, откуда у задачки ноги растут, покажу наглядно:
Имеем некий "ящичек" с заданными внутренними габаритами А х В. И имеем необходимость расположить в нём по диагонали плашку заданной толщины так, чтобы она всеми углами касалась внутренних стенок ящика (то есть "впритык"). Нужно рассчитать длину этой плашки.
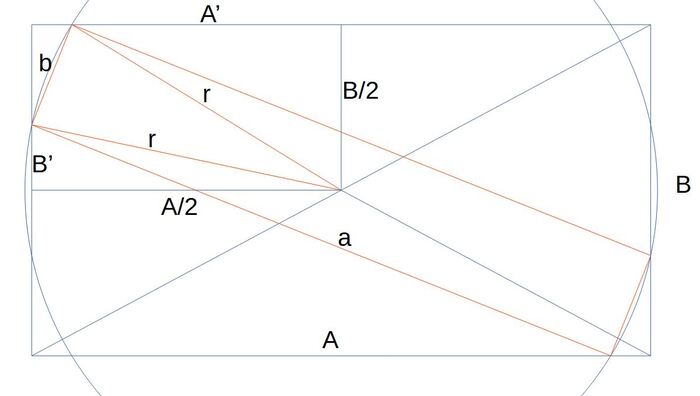
Геометрически задача сводится следующей картинке:
Один прямоугольник вписан во второй. Значения A, B и a - известны, найти значение b.
Башкой понимаю, что решение есть, и ответ абсолютно однозначный. А вот как его найти - хз.
Многие дети (да и взрослые тоже) считают арифметику скучной. Ну что интересного в том, чтобы складывать и вычитать числа?
Но знаете ли вы, сколько в арифметике загадочных и совершенно необъяснимых вещей?
Для начала возьмём так называемую «задачу Эйлера», она же «задача о тридцати шести офицерах», которую, согласно легенде, предложила знаменитому математику Леонарду Эйлеру императрица Екатерина Великая.
София Августа Фредерика Ангальт-Цербстская, более известная как Екатерина II Алексеевна (1729–1796) и Леонард Эйлер (1707–1793)
Чтобы не утомлять вас старинными воинскими званиями, переведём её на простой современный школьный язык.
Итак, пусть у нас есть 36 ребят, поровну учеников первого, второго, третьего, четвёртого, пятого и шестого класса. (По шесть человек получается, верно?) Все они посещают разные кружки и секции. Пускай шестеро из них (кто из какого класса – мы не знаем!) занимаются музыкой, шестеро – танцами, шестеро – рисованием, шестеро – футболом, шестеро – плаванием и шестеро – компьютерами.
Итак, задача: нужно расставить наших ребят в квадрат шесть на шесть так, чтобы в любом ряду – как по горизонтали, так и по вертикали! – были представлены, не повторяясь, ученики всех классов (один первоклассник, один второклассник и так далее до шестиклассника) и всех увлечений (то есть один музыкант, один танцор, один художник, один футболист, один пловец и один юный программист).
Ещё раз подчёркиваем: повторы комбинаций недопустимы, то есть у нас не может быть, скажем двух первоклассников-музыкантов или второклассников-художников.
Попробуйте придумать такую расстановку.
Однако скажем сразу: академик Эйлер бился с этой задачей несколько месяцев – но так и не смог отыскать её решения! Расставить детей в указанном порядке не получится, хоть ты лопни.
Может, эта задача вообще не решается? Вовсе нет. Если мы возьмём эту же задачу для 16 детей (то есть с первого класса по четвёртый, и чтобы увлечений было всего четыре, «от музыканта до футболиста»), то она решается очень просто:
Академик Эйлер сумел решить эту задачу и для 25 ребят (с первого по пятый класс и от музыканта до пловца). В дальнейшем этой задачей занимались тысячи (!) математиков, и в 1959 году было доказано, что эта задача решается для любых квадратных чисел с корнем больше трёх. Любых, кроме тридцати шести!
Как такое может быть? Наша интуиция, наш здравый смысл подсказывает – если задача решается в случае 3 х 3, 4 х 4, 5 х 5, 10 х 10, да хоть 22 х 22 – то она ну просто всенепременно должна решаться для всех чисел n x n! Но нет – для квадрата «шесть на шесть» задача Эйлера неразрешима... Впрочем, как и для квадрата «два на два» (попробуйте сами).
Что же особенного в числах 2 и 6? Почему именно 2 и 6? Почему эта задача не решается именно для этих двух чисел и никаких других? А никто не знает...
А вот другая удивительная задача, сформулированная в 1949 году индийским математиком Даттарая Капрекаром.
Даттарая Рамчандра Капрекар (1905–1986)
Возьмите любое четырёхзначное число, в котором не все цифры одинаковые. То есть 1111, 2222 или 9999 – нельзя. А любые другие – можно. Пусть у нас будет число 2023. Теперь внимание! Переставим цифры этого числа так, чтобы получить самое меньшее возможное число. Нетрудно догадаться, что это будет число 0223, так? А теперь переставим цифры так, чтобы получить самое большое число. Понятно, что это будет 3220, ага? Вычтем меньшее число из большего:
1) 3220 – 0223 = 2997
Сделаем с числом 2997, которое у нас получилось, то же самое: переставим цифры, найдём наименьшее возможное число (2799) и наибольшее (9972). Снова вычтем:
2) 9972 – 2799 = 7173
Продолжаем, повторяем всё то же самое:
3) 7731 – 1377 = 6354
4) 6543 – 3456 = 3087
5) 8730 – 0378 = 8352
6) 8532 – 2358 = 6174
А дальше (глубоко выдохнули) начинается то самое, удивительное!
7) 7641 – 1467 = 6174
8) 7641 – 1467 = 6174...
Всё, наши расчёты навсегда бесконечно «зациклились» на одном-единственном числе 6174!
Можно подумать, что это просто совпадение, случай. Однако нет, не случай. Возьмите совершенно любое четырёхзначное число с не повторяющимися цифрами – хоть 1234, хоть 9876, проделайте те же самые действия – и в итоге всё равно получите всё то же самое «упрямое» число 6174, как говорят математики – «неподвижную точку преобразования».
И снова, как с задачей Эйлера, вопрос: почему?! Как?! Почему все четырёхзначные числа в преобразовании Капрекара «сходятся» к числу 6174? Что в нём такого особенного?
Кстати, можете проверить сами: все трёхзначные числа с неповторяющимися цифрами точно также «сходятся», «сбегаются» к волшебному числу 495. А вот с двухзначными или пятизначными числами у вас этот фокус, как ни бейтесь, не получится. В этом случае «неподвижной точки преобразования» нет!
Дальнейшие проверки на компьютере показали, что для шестизначных чисел таких вот «точек Капрекара» существует две: это числа 549945 и 631764 (если вы узник замка Иф, возьмите карандаш и проверьте сами). А для семизначных чисел «точек Капрекара», «волшебных чисел Капрекара» снова не существует...
Ну как, вы всё ещё считаете, что в математике нет ничего загадочного, да?
P.S. Кстати, задача Эйлера для числа 36 имеет решение с точки зрения квантовой механики – если ученики или их свойства будут находиться в «суперпозиции», то есть, например, если кто-то из учеников окажется одновременно учащимся и первого, и второго класса. Но такое возможно только в микромире, а в макромире нет! А ведь ученики, классы, кружки – это явления макромира, правда?
Отзывы о журнале «Лучик» можно почитать здесь.
