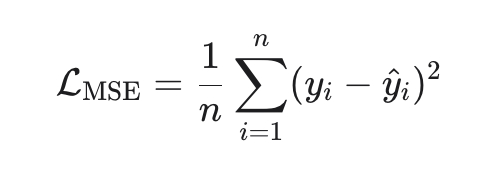Что такое функция потерь?
Что такое оптимизатор Adam?
Делаю такой клиповый курс «Что такое», где за 20 секунд объясняю термины по разработке нейросетей и искусственному интеллекту.
Если пост наберёт 30 плюсов, продолжу выкладывать другие клипы в сообществе «Искусственный интеллект».
Линейная регрессия — один из самых фундаментальных и широко применяемых методов в машинном обучении. Несмотря на простоту, её эффективность сильно зависит от двух ключевых компонентов:
Функции потерь (loss function) — что именно мы минимизируем?
Метода оптимизации (solver) — как мы ищем решение?
В этой статье мы разберём популярные функции потерь — MSE, MAE, Huber и Log-Cosh — их свойства, плюсы и минусы. А также покажем, как выбор функции потерь определяет выбор алгоритма оптимизации.
Функция потерь измеряет, насколько предсказания модели отличаются от реальных значений. От её формы зависят:
Чувствительность к выбросам
Наличие замкнутого решения
Выпуклость задачи
Скорость и стабильность обучения
Давайте сравним четыре ключевые функции потерь в контексте линейной регрессии.
Эквивалентна максимуму правдоподобия при нормальном шуме.
Чувствительна к выбросам (ошибки возводятся в квадрат).
Normal Equation (аналитическое решение)
SGD, SAG, LBFGS (в scikit-learn: solver='auto', 'svd', 'cholesky' и др.)
Когда использовать: когда данные «чистые», ошибки гауссовские, и важна интерпретируемость.
Робастна к выбросам (ошибки в первой степени).
Минимизирует медиану ошибок (а не среднее).
Недифференцируема в нуле → нет аналитического решения.
Требует итеративных методов.
Linear Programming (например, через симплекс-метод)
Subgradient Descent (в scikit-learn: QuantileRegressor с quantile=0.5)
Когда использовать: когда в данных есть аномалии или тяжёлые хвосты (например, цены, доходы).
Гладкая и дифференцируемая.
Робастна к выбросам (линейная штраф за большие ошибки).
Гибкость через параметр δδ.
Нужно настраивать δδ (часто выбирают как процентиль ошибок).
Нет замкнутого решения.
Gradient Descent, LBFGS, Newton-CG(в scikit-learn: HuberRegressor с fit_intercept=True)
Когда использовать: когда вы подозреваете наличие выбросов, но хотите сохранить гладкость оптимизации.
Гладкая везде (бесконечно дифференцируема).
Ведёт себя как MSE при малых ошибках и как MAE при больших.
Устойчива к выбросам, но без «изломов».
Вычислительно дороже (логарифм и гиперболический косинус).
Не так распространена в классических библиотеках.
Gradient-based методы: SGD, Adam, LBFGS(в TensorFlow/PyTorch легко реализуется; в scikit-learn — через кастомный регрессор)
Когда использовать:
когда вы ищете баланс между робастностью MSE и гладкостью MAE.
Вы хотите избежать чувствительности MSE к выбросам, но сохранить дифференцируемость.
Вы строите гибридную модель, где loss должен быть всюду гладким (например, для вторых производных).
Правило:
Если loss квадратичен → можно решить напрямую.
Если loss неквадратичен → нужен итеративный численный метод.
И помните: нет универсально «лучшей» функции потерь — только та, что лучше всего подходит вашим данным и задаче.
Прежде всего, нам необходимо оценить выражения: "2(1+2)"; и: "2а";
А). Одни утверждают, что между числом и скобкой, а также, между числом и буквой,- разрешается записывать знак умножения (точку), а можно точку и не записывать. Это считается одним и тем же выражением. Т. е. всегда соблюдаются тождества: "2(1+2)=2*(1+2)"; и: "2а=2*а";
Решение. По Правилу, решаем пример: слева, направо.
а). 6:2(1+2)=6:2*(1+2)=(6:2)*(1+2)=3*3=9;
б). 6:2а=6:2*а=(6:2)*а=3*а=(при: а=1+2)=3*(1+2)=3*3=9;
Б). Другие считают иначе. Точка не просто так опускается в таких выражениях. Если точка опущена, то это делается намеренно, чтобы показать, что: и: "2(1+2)"; и: "2а"; - это всегда ЕДИНЫЕ выражения. Тогда и решение получим другое:
а). 6:2(1+2)=6:(2+4)=6:6=1;
б). 6:2а=6:(2а)= (при: а=1+2)=6:[2(1+2)]=6:(2*3)=6:6=1;
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Чтобы понять какое решение правильное, необходимо знать и четко различать принятые Стандарты написания тех или иных мат.выражений.
В большинстве стран Мира ( В том числе и в Р.Ф.) предписывается решать примеры со знаками дел. "двоеточие" и знаками умнож. "точка" строго слева, направо. Допускается, предварительно, выполнить операцию в скобках, - если это возможно сделать сразу. Но в данном "Правиле" никак не оговаривается, как требуется оценивать написание, или пропуск написания, точки в таких выражениях. Потому мы можем, как писать точку, так и не писать ее вовсе, - от этого значение выражения НЕ ИЗМЕНИТСЯ.
Вывод: Решение выражений по первому варианту (А) , считается, в названных странах, - правильным решением. То есть, это будут такие решения: "6:2(1+2)=9"; и: "6:2а=9"; при а=1+2;
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
А другое замечание, что знак "точка" не просто так записывается или опускается в мат. выражениях, учитывается уже при оценке совершенно другого стандарта написания мат. выражения, в котором вместо знака "двоеточие" записан другой знак деления, а именно знак: "наклонная" черта. Поэтому сравните выражения:
а). 6/2(1+2)=6/(2+4)=6/6=1; Но уже: 6/2*(1+2)=(6/2)*(1+2)=3*3=9;
б). 6/2а=(при: а=1+2)=6/2(1+2)=6/6=1; Но уже: 6/2*а=(6/2)*а=3*а=(при: а=1+2)=3*(1+2)=3*3=9;
Данный факт мало кто учитывает при анализе решения данных выражений, а преподаватели в начальных классах их, фактически, упорно обходят своим вниманием.
Автор: А. Андреев. (13.12.2025 г.).
У меня в аттестате почти все 5, за редким исключением.
Я теперь даже не помню, по каким предметам было 4.
Но что удивительно- по математике и физике всегда было 5! Всегда.
Между тем, я ничего не смыслю в этих науках.
Те я хорошо решала уравнения, и даже графики к ним рисовала. Но никогда не понимала, что я делаю.
Просто была формула, был пример, как делать - я это усвоила - и просто повторяла.
Из школьной программы я вынесла - умножение/вычитание, сложение, дроби, проценты…. И это все!
Ну да, графики простые могу построить…
Пару лет назад в телеграмм канале наткнулась на энтузиаста, который , играючи, объяснил значение числа Пи.
Для меня это было открытием
И теперь я думаю, что мои преподаватели в школе тоже ни хрена не понимали.
Тоже, видимо, по шаблону работали
****
Хочу дополнить про химию.
В начале учебного года , когда только предмет ввели, я заболела. Недели две меня не было.
С тех пор я вообще не понимаю химию.
Хотя в аттестате 5. Не знаю, как так получилось.
Но! Мне хватило одного раза присутствия на уроке частного репитора, куда я отвела дочь.
О! Чудо! Женщина - препод начала с азов, и я сразу все поняла.
Ну вот как так?
И ещё- в Вузе - с горем пополам что-то сдала. Тоже не особо понимая.
Потом ещё получала ср.спец- там был классный препод. Она с меня три шкуры сняла, пока я сделаю так, как она хотела.
Но результат для меня лично - тот же + ноль.
Как вам такая задача?
Найдите наименьшее натуральное число, десятичная запись которого содержит все цифры от 0 до 5, и которое делится на все эти цифры (нуль не является натуральным числом).
Ссылка на источник задачи: https://mmmf.msu.ru/archive/20102011/z8/22.html
Если понимать буквально, то фраза «делится на все эти цифры» означает, что число делится и на 0. Но деление на 0 не определено вообще, ни для каких натуральных чисел.
Автор, правда, приписала: «нуль не является натуральным числом», но такая приписка не спасает положения. Формально она никак не отменяет того, что нуль всё ещё входит в список цифр, на которые делится число.
Или я чего-то не понимаю?
Я не математик, даже рядом с математиком не стоял. Но из первых предложений твоей статьи, я сразу понял что ты несёшь полную х...ню и мне сразу пришел на ум один старый, но очень мудрый анекдот:
Новое интересное утверждение о том, что LLM решили открытую проблему в математике, заслуживает внимания и подробного разбора. Я попытался разобраться и попытаюсь вкратце рассказать.
Для контекста надо объяснить вначале, что такое "список Эрдеша".
Пал Эрдёш был знаменитым венгерским математиком, невероятно продуктивным, автором более 1400 статей, почти все из них написаны в соавторстве (более 500 различных соавторов из десятков стран). Он коллекционировал и публиковал интересные нерешенные вопросы, чаще всего в теории чисел, комбинаторике, теории графов и теории вероятностей. Сайт "проблемы Эрдеша" собрал список из более 1100 таких нерешенных проблем и отслеживает публикации о них и их статус после его смерти в 1996 (около 40% решены до сих пор).
Не так давно промелькнула новость о том, что ChatGPT нашел решение одной из открытых проблем Эрдеша, и это восторженно обсуждали в соц. сетях полдня или день, пока не обнаружилось, что путем испорченного телефона пропал важный нюанс: он "нашел решение" в том смысле, что "нашел уже существующую старую статью, еще из 1960-х, в которой дается решение, и о которой не знал ни Эрдеш, ни автор сайта проблем". Это несомненно примечательно, и показывает мощь LLM в обработке огромного количества материала, на котором они были натренированы, но все-таки далеко не то же самое, что "сам нашел неизвестное ранее решение". Дошло до того, что один из вице-президентов OpenAI удалил твит, в котором хвастался этим достижением, а другие важные игроки в этой сфере постили саркастические замечания в этой связи.
Сегодняшняя новость не из таких. С помощью Aristotle, новой LLM, которая находит напрямую формальные доказательства математических утверждений (эти доказательства можно потом верифицировать, и если они проходят проверку, считать вопрос закрытым), решена другая открытая проблема с сайта Эрдеша, проблема номер 124. Там действительно не было известно решение. Но... есть нюанс.
В статье 1996 года Эрдеш с тремя соавторами (один из них - Рональд Грэм, другой знаменитый математик) рассмотрел следующую задачу. Возьмем какой-то набор натуральных чисел, например 3,4,5, и рассмотрим все их степени, расставленные по порядку. Эти степени: 3,9,27,81... 4,16,64... 5,25,125,... если их расставить по порядку, выйдет: 3,4,5,9,16,25,27,64,81,125...
Верно ли, что начиная с какого-то числа N, любое число больше N может быть представлено как сумма степеней из этого списка (каждую степень можно брать не больше 1 раза)?
Например, для этого набора 3,4,5 и этого списка степеней можно видеть, что 1,2,6,10 невозможно составить как сумму чисел из этого списка. Дальше есть еще несколько невозможностей, но самая большая из них - 79. В своей статье они доказали, что любое число больше 79 можно представить, как сумму: скажем, 80=64+16, 81=64+9+5+3 итд.
(в статье ошибочно указано 78 вместо 79, я исправил ошибку. 78=64+9+5, 79 нельзя представить)
Что если я возьму какой-то другой набор вместо 3,4,5, ну скажем 10,95,102? Будет ли и тогда, начиная с какого-то числа, возможно представить любое как сумму степеней? Для того, чтобы был шанс на это, нужно как минимум два требования к набору. Во-первых, чтобы наибольший общий делитель всех чисел был 1: скажем, если это не так, и все числа в наборе кратны 3, скажем 3,6,9, очевидно, что любая сумма степеней тоже кратна 3, и невозможно будет *любое* число начиная с какого-то представить как сумму. Это очевидно. Во-вторых, эти числа должны быть в некотором смысле "достаточно маленькими", иначе их степени имеют слишком много "дырок". А именно, должно выполняться неравенство: сумма 1/(x-1) по всем x из набора больше или равна 1. Скажем, набор 3,4,5 это условие выполняет: 1/2 + 1/3 + 1/4 больше 1. А набор 10,95,102 не выполняет, и поэтому с ним шанса нет. Это условие не так очевидно, но можно доказать, что оно необходимо, стандартными средствами теории чисел.
Так вот, если я возьму набор чисел, который выполняет эти два условия, будет ли ТОГДА гарантировано, что начиная с какого-то числа все можно записать как сумму степеней набора? Это и есть открытая проблема, которую сформулировали
Эрдеш с соавторами в этой статье. Они не смогли ее решить в общем случае - только для некоторых наборов, как например 3,4,5.
А новый LLM "Аристотель" от компании Harmonic смог ее решить, нашел доказательство там, где не справились Эрдеш, Грэм и еще двое математиков? Так? Не совсем так. Есть нюанс.
Когда я сказал "возьмем список всех степеней каждого числа из набора", я начал с ПЕРВОЙ степени: 3,9,27... 4,16,64... Можно понять это по-другому и начать с НУЛЕВОЙ степени, которая всегда равна 1: тогда список степеней будет такой: 1,1,1,3,4,5,9,16,25,27,64,81,125... Три единицы в начале, потому что отдельно можем брать нулевую степень от 3, 4 и 5. Зададим тот же вопрос: можно ли любое число, начиная с какого-то, записать как сумму степеней из этого списка, если набор выполняет два условия выше.
Именно в таком виде, "с единицами", статья сформулирована на сайте "проблемы Эрдеша". Как это вышло? Ну дело в том, что статья 1996 года не была единственным источником этой задачи; в следующем году Эрдеш опубликовал небольшую обзорную статью "Problems in Number Theory" в журнале новозеландской математики (публиковать во всяких рандомных журналах было для него нормальным делом), где свел вместе несколько нерешенных проблем, включая эту. В этой статье он не указал условие "наибольший общий делитель равен 1", а насчет того, какая степень первая, 0 или 1, написано немного неясно. Видимо, составитель сайта именно из этой статьи взял точную формулировку проблемы: у него тоже нет требования про наибольший общий делитель, а степень указана с нуля, т.е. список степеней "с единицами".
Так вот, оказывается, что у задачи "с единицами" есть очень простое элементарное доказательство, причем гораздо более сильного факта: что ЛЮБОЕ число (а не "начиная с какого-то") можно представить как сумму из списка степеней. И именно это доказательство нашел Аристотель. Единицы оказываются очень сильным подспорьем. И условие по наибольшему общему делителю тоже оказывается ненужным - нужно только по сумме 1/(1-x).
Что же в итоге доказано? Скажем так, есть исходная статья 1996 года, где соавторы сформулировали Г1 (Гипотезу-1). Есть статья Эрдеша 1997 года, где он дает немного другую формулировку, которую можно прочитать как Г2 (Гипотеза-2), хотя он говорит, что всего лишь повторяет задачу из статьи 1996 года. Именно в виде Г2 задача лежит много лет в списке нерешенных задач Эрдеша, со ссылкой на все три статьи, пока не приходит человек и с помощью LLM не находит очень простое решение.
Мне кажется, что в статье 1997 года Эрдеш просто небрежно сформулировал, но все-таки имел в виду Г1. А задача Г2, хоть и висела на сайте много лет, либо не получала почти внимания математиков, либо те шли читать исходную статью-1996 и пытались решать тяжелую задачу Г1. Если бы математик-специалист задумался именно над Г2, как над свежим отдельным утверждением, без контекста тяжелой задачи Г1 и сложных методов, которые к ней применялись, то скорее всего быстро бы решил ее.
В свете этого то, что найдено простое решение Г2, приятно и красиво, но гигантским шагом вперед я бы не назвал. Вот так примерно. Буду рад поправкам и предложениям от экспертов.
P.S. Вот суть простого доказательства Г2, которое нашел LLM. Сказать, что любое число можно представить в виде суммы из данного списка степеней, эквивалентно тому, что сумма первых N степеней из этого списка, для любого N, больше или равна следующей степени минус 1. Например, напомню список степеней "с единицами" для набора 3,4,5:
1,1,1,3,4,5,9,16,25,27...
Мы видим, чтo первое число не меньше второго минус 1. Сумма первого и второго не меньше третьего минус 1. И так далее, скажем 1+1+1+3+4+5+9 >= 16-1. Если мы это докажем для любого n, из этого легко следует, что любое число можно представить как сумму (подробности опускаю, но могу объяснить, если надо).
Но сумму скажем первых десяти членов можно разбить на геометрические прогрессии: 1+3+9+27, 1+4+16, 1+5+25. Сумма каждой прогрессии равна (d^n-1)/(d-1), это из школьной программы: в данном случае это (81-1)/(3-1), (64-1)/(4-3), (125-1)/(5-1). Если мы в этой сумме все числители заменим на наименьший из них, тут это 64-1, то получим что-то меньше. Вынеся это за скобки, получим сумму по всем числам набора 1/(x-1), которая по условию больше или равна 1, так что заменив всю сумму на 1, опять уменьшим.
Короче, число 64-1 меньше, чем вся эта сумма первых десяти членов. Но следующее число в списке как раз наименьшее из еще отсутствующих в нем степеней - как раз 64 в этом примере. Поэтому сумма первых десяти больше или равна одиннадцатому минус 1, 64-1. И так для любой суммы первых n членов.
Ссылки по теме: страница на сайте проблем Эрдеша, статья 1996 года, статья 1997 года.
