Карты

Немного истории. Всем известна плоская карта мира и наверное большинство знает, что судить о расстоянии между двумя точками по ней не стоит. Все потому, что расплющить шар без искажений нельзя. Наиболее известная попытка, которая до сих пор используется, была сделана в 1569 году Герадусом Меркатором (https://en.wikipedia.org/wiki/Mercator_projection) и вот здесь видно как она искажает расстояния (кружки на самом деле одинаковы):

Сравните Австралию с Гренландией, а Антарктида вообще занимает пол мира :-)

Было сделано много попыток улучшить проекцию (так по научному называется натягивание ... ну в общем создание плоской карты мира :). До сих пор лучшем вариантом считалась проекция Освальда Винкеля предложенная в 1921 (https://en.wikipedia.org/wiki/Winkel_tripel_projection):

Для оценки проекций используется довольно стандартный метод, придуманный великим математиком Карлом Фридрихом Гауссом - сумма квадратов ошибок. Правда для картографических проекций этот метод напрямую не подходит - всегда есть места, где ошибка  бесконечна (например на полюсах). Поэтому Гольдберг и Готт  предложили измерять ошибку в шести  зонах, так называемая оценка по Гольберг-Готт (https://www.physics.drexel.edu/~goldberg/projections/):

Естественно для глобуса эта оценка - 0.000, а вот для проекций ...  у Меркатора - 8.296, у Винкеля почти вдвое лучше - 4.563. Вот тут несколько вариантов проекций и их оценки:

(колонки - это 6 зон по Гольберг-Готт, их надо суммировать для вычисления самой оценки)

Как видим ученые и картографы не унимаются и с 1569 напридумывали много чего. Но попытки продолжаются. В феврале 2021-го была опубликована новая проекция от того самого Готта. Ошибка - 0.881, в 9.5 раз лучше Меркатора и в 5 раз лучше Винкеля прочем лучше по всем 6 зонам! Правда у нее есть один недостаток - карт две, а не одна:

Как заявил сам автор: "карта Винкеля хорошо смотрится на стене, но моя более аккуратна в ваших руках"

Источник: https://www.scientificamerican.com/article/the-most-accurate...

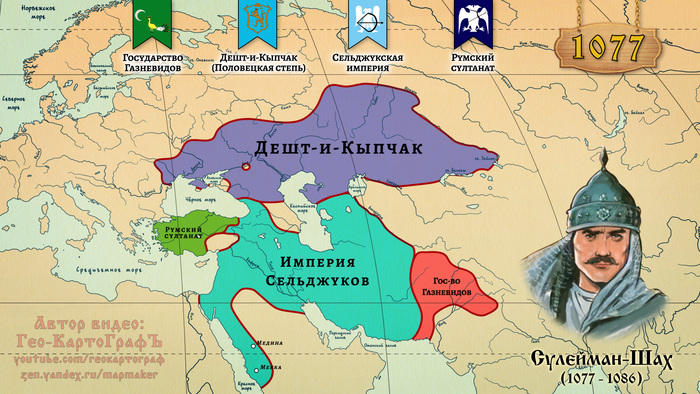
В первой части видео вы сможете познакомиться с историей таких великих тюркских государств, как Великая империя Хунну, Западная империя Хунну, Европейская империя Гуннов, Империя Белых Гуннов (Эфталитов), Тюркский каганат, Аварский каганат, Хазарский каганат, Уйгурский каганат, Кыргызский каганат, Огузская держава, Караханидское ханство, Государство Газневидов, Дешт-и-Кыпчак, Сельджукская империя, Румский султатат, Хорезм.

Данный таймлайн основан на концепции 16 великих тюркских империй. Я дополнил эту концепцию ещё несколькими государствами, достойными сего рейтинга.

Ознакомиться с видео можно на канале Гео-КартоГрафЪ.

Если вам понравилось видео, которое можно посмотреть здесь, поддержите меня подпиской.

Свои пожелания для второй части видео, можете оставить в комментариях под этим постом.

Естественно все мои стили для карты в этом месте летят к чертям. Это должна быть контрастная карта очертаний, без каких либо названий и лишних пометок. Но этот кусок все портит. Можно ли как-нибудь отключить эту фичу? Ведь на предыдущем приближении такой замены нет:

Такая замена происходит при приближении 7 и больше, но у 6 приближения недостаточная детализация. Как это можно обойти?