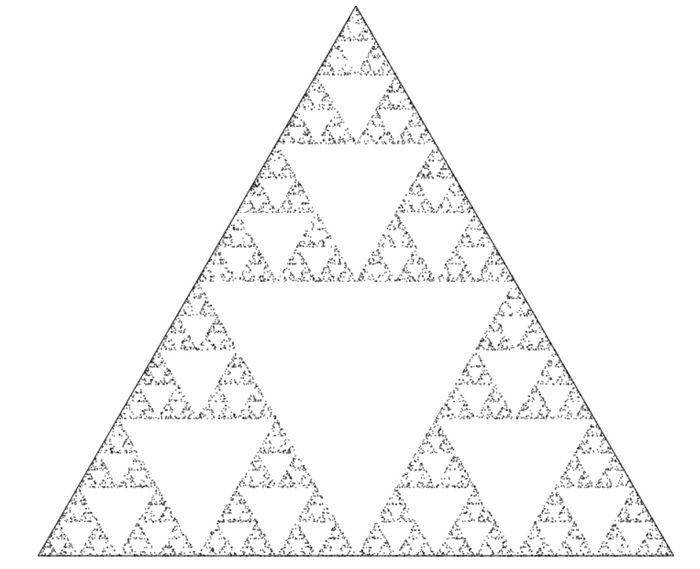
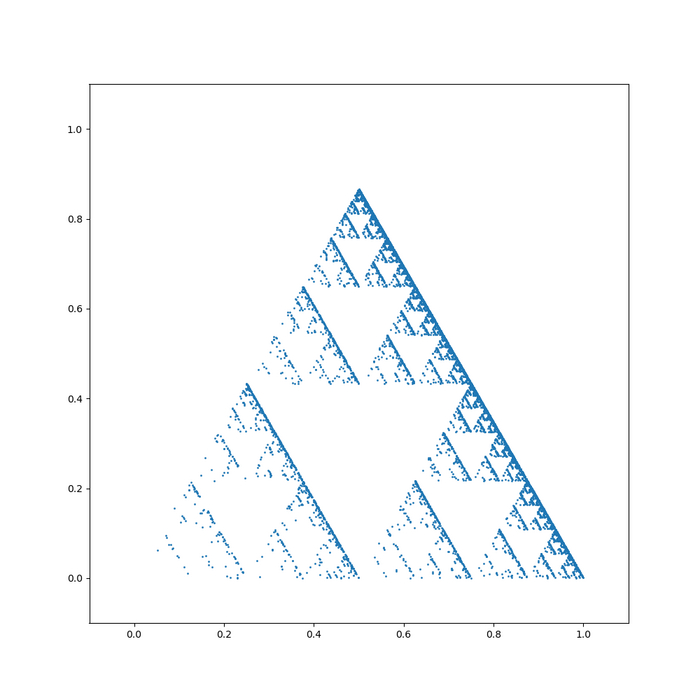
Треугольник Серпинского за 439 символов
Дело было вечером, делать было нечего. Наткнулся на статью, где описывался алгоритм построения треугольника Серпинского, и решил реализовать и максимально сжать.
Создать файл html и вставить туда код:
<canvas id=c><script>a=[],s=400,t=0,u=3,M=Math;for(i=-0.5;i<u;){r=M.PI*2*i++/u;a.push({x:M.sin(r)*s+s,y:M.cos(r)*s+s})}e=document.getElementById("c");e.width=e.height=2*s;c=e.getContext("2d");c.beginPath();a.forEach(q=>c.lineTo(q.x,q.y));c.stroke();q=()=>a[M.round(M.random()*u)],v=(a,b)=>b+(a-b)/(u-1),p=q(),e.onclick=n=()=>{t=t?clearInterval(t):setInterval(()=>{s=q();p={x:v(p.x,s.x),y:v(p.y,s.y)};c.fillRect(p.x,p.y,1,1)})};n()</script>
u - количество углов (можно увеличить)
при нажатии анимация останавливается и восстанавливается.
Уменьшить размер не потеряв функциональность пока не получилось
Ответ randomnik в «Если есть свободное время, то можете нарисовать треугольник Серпинского»4
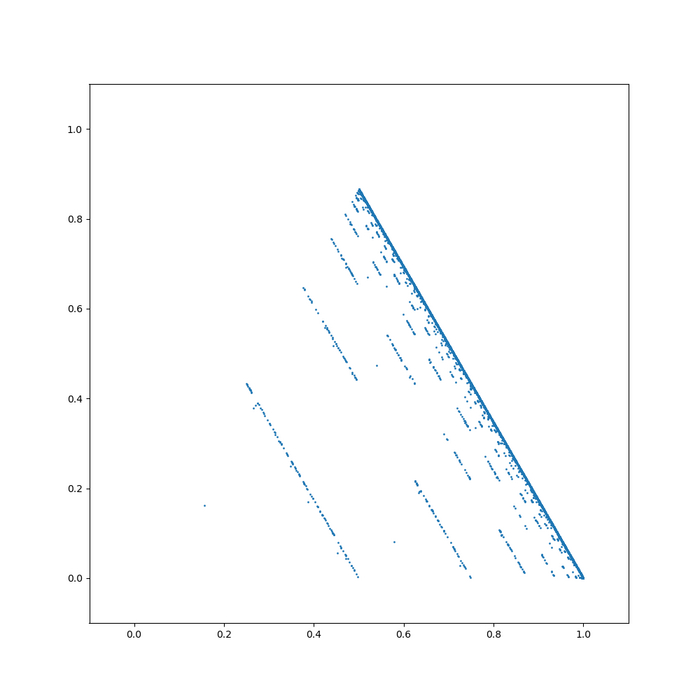
Как ещё один математик-любитель, вставлю свои пять копеек :) Как справедливо заметил автор, остался нераскрытым такой вопрос: почему наши точки покрывают красную зону равномерно? Если мы будем бросать "нечестную" игральную кость, то картинки будут совсем другие:
Здесь мы выбираем левый нижний угол всего в 1 случае из 10. И сразу же ощущение "сдохшего картриджа" :) А если брать левый нижний угол в 1 случае из 100, получится вообще вот так:
Но далеко не всегда неравные вероятности портят результат. Например, в "папоротнике Барнсли" (см. https://en.wikipedia.org/wiki/Barnsley_fern - на русской вики удивительно мало текста) это не баг, а фича (картинка оттуда же, из википедии):
Вообще, процесс на видео называется "Игра хаоса" (https://en.wikipedia.org/wiki/Chaos_game). О том, почему это работает, достаточно кратко написано вот здесь: https://core.ac.uk/download/pdf/82248898.pdf . Но это доказательство достаточно формальное и не даёт, на мой вкус, понимания сути происходящего. Для этого нужно погрузиться в теорию эргодичности (https://ru.wikipedia.org/wiki/Эргодичность). Она же даёт нам ответ на вопрос "А почему, собственно, мы имеем право рассуждать о поведении молекул газа или жидкости с помощью статистики и вероятностей, если отдельные молекулы ведут себя предсказуемо и подчиняются второму закону Ньютона?" Но про эргодичность я практически ничего не знаю, засим и откланиваюсь :)
Ответ на пост «Если есть свободное время, то можете нарисовать треугольник Серпинского»4
Под этим постом было какое-то количество комментариев про магию что задело меня, как математика-любителя, поэтому я решил попытаться немного развеять эту магию и, надеюсь, переубедить хотя бы какое-то количество людей, что магии в нашем мире нет и все можно объяснить, подумав достаточное количество времени.
Вкратце, о чем был этот пост: если на плоскости нарисовать треугольник, выбрать в внутри него точку, а затем выбирать какую-то вершину треугольника и "приближать" точку к выбранной вершине на половину расстояния, то со временем точки начнут образовывать фигуру, подозрительно похожую на треугольник Серпинского.
Чудо/магия – скажет обычный человек
А чего вы еще ожидали? – скажет математик
Итак, сейчас я попытаюсь вас убедить, почему ничего, кроме треугольника Серпинского, получиться при таких действиях не могло.
Давайте посмотрим, где могла оказаться первая точка и как выглядит множество возможных положений второй, третей и т.д. точек
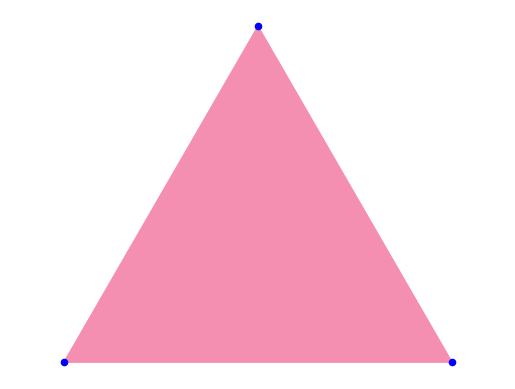
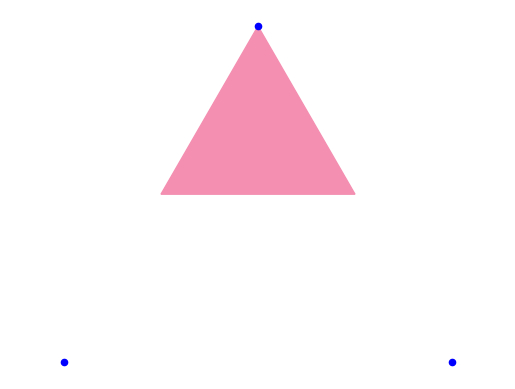
По условию первую точку мы выбираем где-то в треугольнике, т.е. множество всех возможных ее положений – весь треугольник:
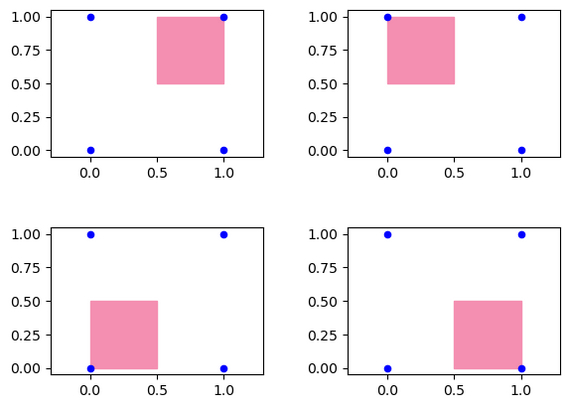
Если мы в качестве вершины, к которой "притягиваем" точку, выберем верхнюю вершину, то точка может переместиться только в эту область:
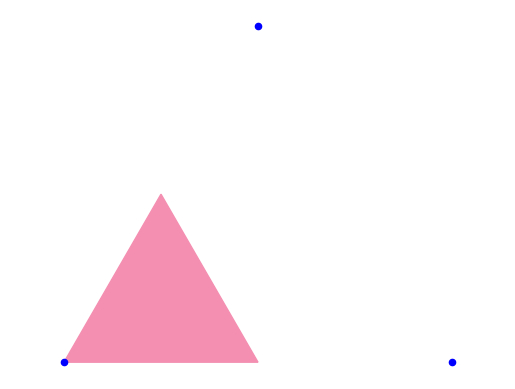
Если выберем левую-нижнюю, то сюда:
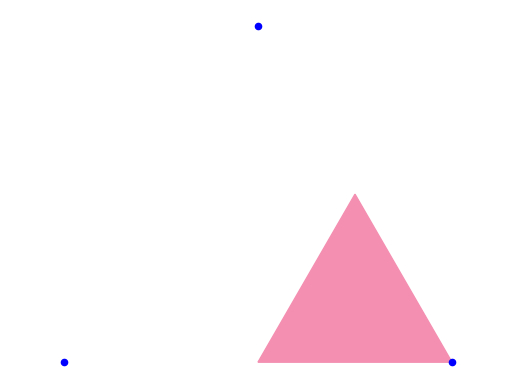
А если правую-нижнюю, то сюда:
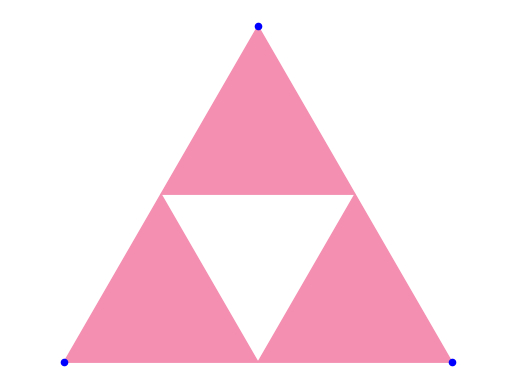
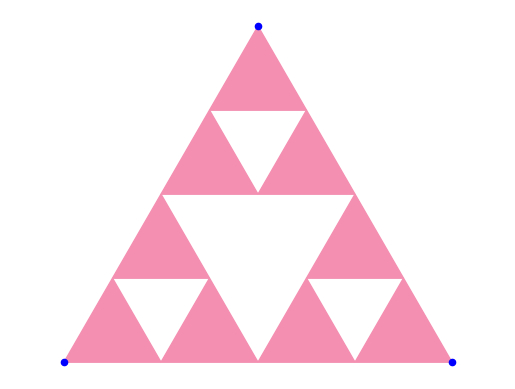
Так как можно выбрать любую из вершин, точка может переместиться в любую из областей, т.е. после одного "перемещения" точка может оказаться только в одной из красных областей:
Где она может оказаться после второго "перемещения"? Нужно "стянуть" красную область к каждой из вершин и объединить полученные области:
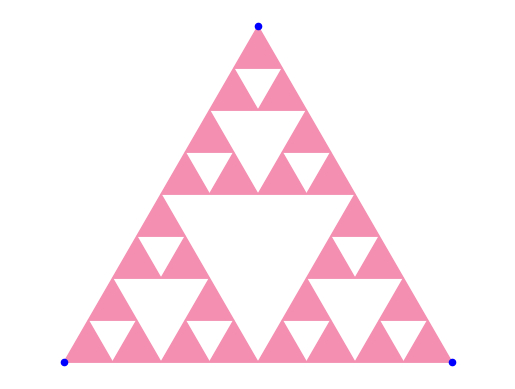
Начинаете что-то замечать?) Продолжая такие манипуляции, можно получить множество точек, где точка может оказаться после трех перемещений:
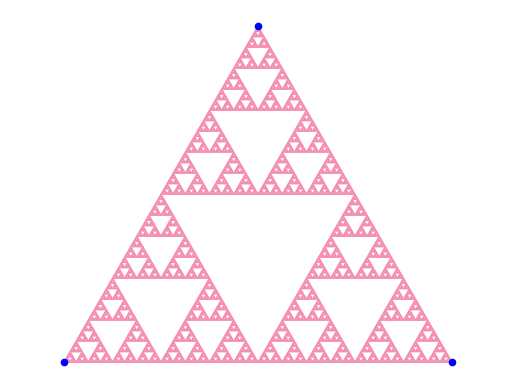
После 7 перемещений точка может оказаться только тут:
То есть у всех белых областей нет другого варианта, кроме как оставаться белыми!
Из этих же соображений следуют и ответы на вопросы вида "что если взять начальную точку где-то в большом белом треугольнике"? Ну, сначала точка будет в нем, но после первого перемещения ее там не будет, после второго перемещения ее точно не будет в белых треугольниках поменьше и так далее. То есть после каждого перемещения точке "запрещается" быть во все более и более маленьких белых треугольниках. Конечно, выбор неудачной начальной точки может подпортить красивую картинку, но в не очень большом количестве заметных для человеческого глаза мест.
Из подобных соображений можно понять, почему для квадрата, вместо красивой картинки, получается шум. После одного перемещения точка может оказаться в одной из этих областей:
Их объединение дает изначальный квадрат, то есть белых областей не появляется и точка по-прежнему может находиться в любой точке квадрата. Но если "притягивать" точку сильнее, чем на половину длины, белые области начнут появляться и картинка станет фрактальной:
Из-за сжатия может показаться, что это не фрактал, но это фрактал, поверьте мне)
На этом все, спасибо, за уделенное время, надеюсь, что мне удалось немного развеять непонимание вокруг этого феномена
P.S. На самом деле, мы показали лишь то, что белые области в треугольнике Серпинского будут белыми и на нашей картинке, но не показали, что каждая точка в треугольнике Серпинского будет закрашена (т.е. то, что получиться именно треугольник Серпинского, а не его подмножество). Объяснения этого факта, в лучших традициях, остается любопытному читателю в качестве упражнения
Гифка с фурами нервно курит в сторонке1
P.s на видео треугольник Серпинского