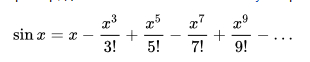Операции сравнения можно оптимизировать до операции вычисления сдвига в памяти до нужного ответа.

Саму таблицу оптимальнее делать размерами 64 х 128 = 8 192. Если мало, то 128 х 128 = 16 384 ячейки.

Вычислить X+Y*128 и получим номер ячейки.

Y*128 можно заменить на операцию сдвига Y << 7 (7 раз сдвинуть влево).

Если ответ занимает 2 байта в памяти с максимальным значением 16 384, то вся таблица 128 х 128 займет 65 536 байт.

Таким образом, для перемножения чисел до 128 потребуется 1 операция сложения, 1 операция сдвига и 64к памяти (65 536 Кбайт)

Для таких простых действий не сильно оптимально подобным заморачиваться. Но вот для вычисления синусов и косинусов для значений от 0 до 180 градусов можно разбить на отрезки 180 / 128 = 1,4 градуса и сделать таблицу 2 х 128 со значениями тригонометрических функций. Даже если результату дать 8 байт под ответ, то вся таблица займет 2048 байт. С существенной экономией для вычисления тригонометрических функций.

Подобное было актуально во времена, когда все хотели 3д игры, но были проблемы с математическими сопроцессорами, ответственными за тригонометрию, да и мощность видеокарт под вопросом. А так заводишь табличку в 2048 байт и вуаля -- можно реализовывать собственные тригонометрические функции!

целочисленное деление: текущий градус * 10 / 14 = номер позиции в таблице.

Можно еще дальше пойти и сделать значения через каждые 0,8 град. Заменив деление на двоичный сдвиг 3 раза или один на 3 разряда.

180/0,8 = 225 значений. Таблица вырастет до 3 600 байт.

Можно еще вспомнить, что синусы и косинусы можно считать друг через друга, т.к. достаточно сдвинуть аргумент на 90 градусов или пи/2.

Итоговая формула: Номер ячейки[(Текущий градус + 90) * 10 >> 3]; таблица размером 1 800 байт.

А сами значения функций вычислять с помощью разложения в ряд. Для синуса на картинке:

1 раз выполняется подобная трудоемкая операция, если нет реализации тригонометрии в вашем математическом сопроцессоре, после чего вы можете сформировать аналог таблиц Брадиса и пользоваться уже в каждом такте. Особенно это было важно для отрисовки кадров, что для разрешения 640 х 480 х 30 fps требовалось 9 216 000 графических операций (для каждого пикселя) или 9,1М вычислений. Не путать с примитивными операциями, тут на каждый пиксель формула для расчета! На совеменных процах с их 3ГГц можно реализовывать графический движок вообще на проце, это для разрешения 640х480х30fps.

Думаете, что это все неактуально? Полно микрочипов, типа управляющих чипов шаговых двигателей, для которых проще именно такую реализацию сделать, если нужно, чтобы чип получал угол в градусах, а чип давал команду насколько сильный ток нужен, чтобы повернуть на необходимый угол. Или для запуска Doom на кофеварке.

Опять же, подобная хитрость с сохранением результата вычисления сложных функций работает и для сложных расчетов. Нужно выяснить шаг, диапазон значений, размер результата функции.

А дальше:

размер результата * диапазон/шаг =...

Если тут получается приемлимый результат по сравнению с длительностью операций, то вполне имеет смысл заводить подобную операцию.

Например, диапазон с 1 угловой минутой от 0 до 90 градусов, это от 0 до 5 400 угловых минут, всего значений 5401 (включая нулевое). Для 8 байтового результата это 43 208 байт в таблице.

Соответственно, если память для хранения 43 208 байт таблицы дешевле, чем находить результат тригонометрической функции каждый раз, то проще завести таблицу.

Сюда же можно записать алгоритм умножения целых чисел через сдвиги:

Если множать числа 13 и 17, то

меньше из чисел представить в двоичной форме // для проца оно итак в двоичной форме

Это число 13 в двоичной форме: 1101

Расчет слева направо:

Итоговый результат итог = 0, к нему прибавить промежуточный результат temp = 17 * 1, итог = 17

Предпоследняя цифра в 1101 -- ноль, просто промежуточный результат удвоить temp = temp >> 1, т.е. 17 * 2

Потом видим единицу, это temp = temp >> 1, т.е. 17 * 4 = 68, добавить к итогу = итог + 68 = 17 + 68 = 85.

Снова единица, это temp = temp >> 1, т.е. 17 * 8 = 136, добавить к итогу = итог + 136 = 17 + 68 + 136 = 221.